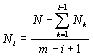В.С.Костин, А.Н.Нуртдинов, А.С.Жданов, Ю.Г.Корнюхин

Бета-регрессия как метод восстановления условного распределения случайной величины

Распределение случайной величины дает наиболее полное статистическое описание наблюдаемых объектов. В работе рассматривается метод восстановления функции условного распределения случайной величины x путем ее аппроксимации Бета-распределением. Коэффициенты Бета-распределения a и b отыскиваются в виде функций от произвольного параметра z. Зависимости a(z) и b(z) аппроксимируются одномерными кубическими сглаживающими сплайнами. Определение оптимальной степени сглаживания рассматривается как статистическая задача о распределении регрессионных остатков. Регрессионные остатки измеряются значимостью отклонения эмпирического условного распределения от теоретического (восстановленного) по непараметрическому тесту Колмогорова-Смирнова. Возможности метода проверяются на специально сгенерированных тестовых выборках различного объема.

Постановка задачи

Данная работа является развитием идеи П.С.Ростовцева [1, с. 121-122] и поддерживается грантом РГНФ №02-02-00216a.

Входными данными для рассматриваемого метода восстановления двумерного распределения является выборка из N наблюдений, описываемая случайными величинами x и z. Предполагается, что x изменяется в интервале (0,1) и условная плотность распределения f(x|z) может быть аппроксимирована Бета-распределением с параметрами a(z), b(z):

(1)

Зависимость параметров a и b от z может быть достаточно сложной. Поэтому для ее восстановления необходимо выбрать класс функций, позволяющий строить приближение практически любой функции и при этом полностью контролировать точность аппроксимации. С учетом этих требований мы выбрали кубические сглаживающие сплайны, математический аппарат построения которых описан в [2, с.54-58 и 3, с. 194-213], а программный код открыто выложен в интернете [4].

Первым шагом восстановления двумерного распределения является выбор значений z_i, i={0,1, … , m}, которые разбивают весь диапазон изменения z на интервалы (z_i-1,z_i). Число интервалов выбирается, исходя из двух противоположных требований. Во-первых, каждый интервал должен быть достаточно широким (содержать много наблюдений), чтобы получить хорошие оценки значений a_i и b_i. Во-вторых, интервалы не должны быть широкими, чтобы не терять информацию о зависимости a и b от z в процессе усреднения. Итак, следует избегать как слишком малого числа интервалов, так и слишком большого.

Кроме количества интервалов, необходимо выбрать и способ разбиения. Здесь существует по крайней мере два решения.

Во-первых, сетка с равномерным шагом, где шаг сетки:

h=(zm-z0)/N

(2)

Во-вторых, сетка с равнонаполненными ячейками, где объем i-ой ячейки:

i={1,…, m}

(3)

Процедура разбиения немного усложняется в том случае, когда наблюдения с одним и тем же z оказываются в разных ячейках.

Если наблюдения распределены равномерно по z, то имеет смысл выбрать равномерную сетку, если же нарушения равномерности существенные, то лучшим вариантом будет разбиение по квантилям.

После разбиения выборки на ячейки по z, можно переходить к вычислению a_i и b_i для каждой ячейки i={1, … , m}. Получить оценки параметров a_i и b_i проще всего методом моментов:

	(4)
	(5)

где - выборочное среднее x, а - выборочная дисперсия (смещенная).

Альтернативный способ получить оценки a и b основан на процедуре максимизации функции правдоподобия, имеющей смысл вероятности совместного наблюдения выборочных данных x_j при имеющейся плотности распределения (1):

(6)

Учитывая ограничения точности и диапазона представления чисел в компьютере, удобнее оптимизировать не саму функцию правдоподобия, а ее логарифм, вместо произведения накапливая суммы:

(7)

Генерация исходных данных

Для проверки работоспособности метода необходимо большое количество выборок с точно известным распределением в генеральной совокупности. Отсутствие реального источнока данных требуемого объема, разнообразия и качества вынуждает обратиться к альтернативному источнику - методу Монте-Карло, то есть искусственной генерации данных с использованием датчика псевдослучайных чисел. Такой подход хорош тем, что позволяет практически мгновенно получать выборки произвольного размера, в точном соответствии с теоретически заданными параметрами распределения на генеральной совокупности.

Процедура генерации выборки включает следующие шаги:

1. Задание границ изменения z: (z_min, z_max).

2. Задание функциональной зависимости a(z) и b(z).

3. Задание объема выборки N.

v Генерация каждого из N наблюдений:

4. Генерация псевдослучайного числа z в интервале (z_min, z_max).

5. Определение параметров Бета-распределения по z: a(z) и b(z).

6. Генерация псевдослучайного числа P в интервале (0, 1). Здесь P имеет смысл вероятности.

7. Определение x, при котором интегральная функция распределения принимает значение P:

(8)

8. Добавление полученных значений {z, x} к выборке.

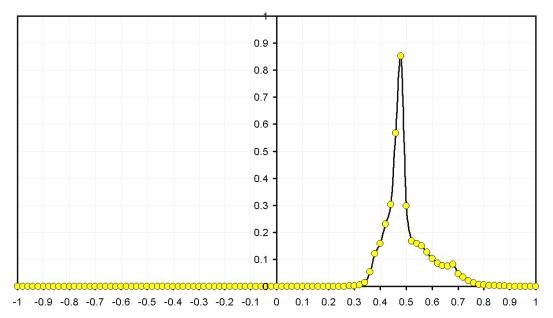
Проиллюстрируем выполнение этой процедуры на примере.

1. Границы изменения z:

Ø z_min = 0, z_max = 100.

2. Зависимости a(z) и b(z):

Ø a(z) = 0.5 + 0.05•z	(9)
Ø b(z) = 5.5 - 0.05•z	(10)

3. Объем выборки N:

Ø N = 400

v Генерируем первое из 400 наблюдений:

4. Генерируем случайное число z в интервале от 0 до 100:

Ø Z = 73.009

5. Определяем параметры Бета-распределения:

Ø a(73.009) = 0.5 + 0.05•73.009 = 4.150

Ø b(73.009) = 5.5 - 0.05•73.009 = 1.850

6. Генерируем случайное число P в интервале от 0 до 1:

Ø P = 0.354463126

7. Определяем x, при котором интегральная функция распределения принимает значение P = 0.354463126:

Ø x = 0.6394

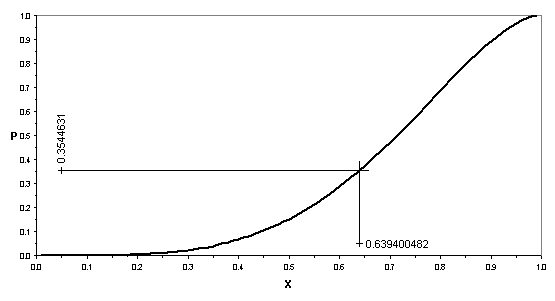Рисунок 1. Преобразование равномерно распределенного случайного числа P в наблюдаемое значение x по Бета-распределению F(x,a(z),b(z))

8. Добавляем полученные значения {z=73.009, x=0.6394} к выборке:

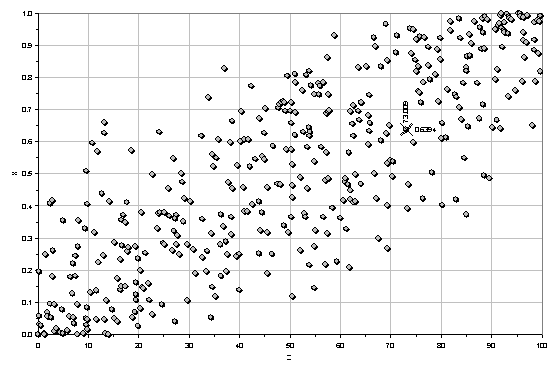Рисунок 2. Выборка из 400 наблюдений по Бета-распределению с параметрами (9, 10). Крестиком обозначено наблюдение {z=73.009, x=0.6394}.

Разбиение на интервалы и оценивание параметров распределения

Как уже было сказано выше, первым шагом восстановления двумерного распределения является задание сетки z_i, i={0,1, … , m}. Здесь z₀ = z_min, а z_m = z_max. Количество ячеек m должно быть таким, чтобы внутри каждой ячейки было достаточно наблюдений для вычисления a_i и b_i. Если сетка с постоянным шагом не позволяет вычислить параметры во всех ячейках, можно, во-первых, уменьшить m, увеличив наполненность ячеек, а во-вторых, перейти к сетке с равнонаполненными ячейками. В этом случае z_i определяется как значение квантиля i/m.

После того, как интервалы будут получены, можно приступать к расчету a_i и b_i. Для этого достаточно вычислить на каждом интервале среднее значение и смещенную оценку дисперсии :

	(11)
	(12)

После этого можно рассчитать a_i и b_i, применив формулы (4) и (5). Если мы хотим получить оценки методом максимального правдоподобия, необходимо найти максимум логарифма функции правдоподобия (7). А в качестве начального приближения при поиске максимума можно воспользоваться только что полученными (методом моментов) оценками a_i и b_i.

При разбиении приведенной выше выборки на 10 равных интервалов мы получим следующие результаты:

Zi-1-Zi	0-10	10-20	20-30	30-40	40-50	50-60	60-70	70-80	80-90	90-100
Ni	46	41	35	33	39	52	44	31	37	42
	5.11	15.56	25.17	35.57	44.86	54.20	64.87	75.51	85.08	94.79
	0.130	0.239	0.300	0.379	0.510	0.562	0.585	0.767	0.769	0.899
	0.019	0.032	0.021	0.035	0.031	0.042	0.033	0.028	0.033	0.012
ai^z	0.755	1.278	1.759	2.279	2.743	3.210	3.744	4.275	4.754	5.239
ai^moment	0.638	1.099	2.695	2.145	3.581	2.737	3.718	4.201	3.418	6.129
ai^maxL	0.563	0.853	2.442	2.262	3.748	2.900	3.516	5.162	3.396	6.081
bi^z	5.245	4.722	4.241	3.721	3.257	2.790	2.256	1.725	1.246	0.761
bi^momen	4.265	3.503	6.299	3.508	3.438	2.129	2.637	1.275	1.024	0.692
bi^maxL	3.860	2.839	5.786	3.663	3.634	2.295	2.439	1.599	1.001	0.682

где Z_i-1-Z_i - границы ячейки, N_i - число наблюдений в ячейке, - среднее значение z в ячейке, - среднее значение x в ячейке i, рассчитанное по формуле (11), - смещенная оценка дисперсии в ячейке (12), a_i^z - теоретическое значение, рассчитанное по формуле (9), a_i^moment - оценка a_i по методу моментов (4), a_i^maxL- оценка a_i по методу максимального правдоподобия, b_i^z - теоретическое значение, рассчитанное по формуле (10), b_i^moment - оценка b_i по методу моментов (5), b_i^maxL- оценка b_i по методу максимального правдоподобия.

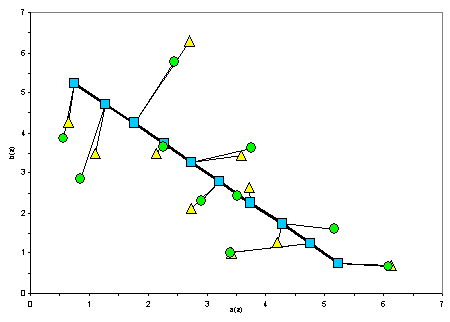
Рисунок 3. Параметры Бета-распределения a_i и b_i: квадраты - теория, треугольники - метод моментов, кружки - метод максимального правдоподобия.

Как видно из таблицы и рисунка, параметры распределения, восстановленные по случайной выборке, достаточно сильно отклоняются от теоретически заданных. Видно, что не сохраняется монотонность изменения параметров распределения. Иными словами, в восстановленном таким путем двумерном распределении слишком велик уровень статистического шума, который не позволяет увидеть теоретически заложенной в выборке линейной зависимости a и b от z. Этот шум обусловлен случайным характером формирования выборки и не может быть преодолен иначе, как увеличением ее объема.

В данной работе мы ставим перед собой задачу найти такой способ восстановления параметров Бета-распределения, который позволит максимально точно восстановить как отдельные значения, так и характер зависимости a и b от z, сведя к минимуму разрушительное действие статистического шума.

Аппроксимация параметров распределения сглаживающими сплайнами

Чтобы решить поставленную задачу, необходимо найти класс функций, позволяющий аппроксимировать эмпирические данные с контролируемой степенью точности, то есть с произвольно заданной ошибкой аппроксимации. Чем выше точность (меньше допустимая ошибка), тем ближе будет аппроксимирующая функция к эмпирическим точкам. Но, как мы видели на рисунке, точность воспроизведения эмпирических значений далеко не то же самое, что точность воспроизведения теоретически заложенной зависимости, поскольку эмпирические значения в значительной степени поражены статистическим шумом. Должна существовать некоторая оптимальная степень сглаживания, которая бы позволила отсеять шум, сохранив при этом заложенную в данных теоретическую зависимость. Естественно, что восстановленная зависимость будет отличаться от теоретической. Задача состоит в том, чтобы это отклонение минимизировать.

Поиск необходимого класса функций начался с полиномов, коэффициенты которых легко определяются из требования минимизации суммы квадратов отклонений значений полинома от эмпирических точек. Но аппроксимация полиномами обладает весьма существенными недостатками.

Во-первых, для полиномов легко подобрать примеры практически неаппроксимируемых функций. В качестве такого примера можно привести ступенчатую (S-образную) кривую с длинными хвостами. Ни один полином конечной степени не в состоянии дать ее удовлетворительное приближение.

Во-вторых, для сглаживания полиномами нет другой возможности управлять степенью сглаживания, кроме изменения степени полинома. А это очень грубая настройка хотя бы в силу того, что она дискретна.

В то же время в последние десятилетия интенсивно развивается новый раздел современной вычислительной математики - теория сплайнов. Сглаживающие сплайны позволяют не только хорошо интерполировать функции по отдельным точно заданным значениям, но и эффективно строить аппроксимацию эмпирических данных с заданной точностью. При минимальной точности мы получаем чисто линейную зависимость с равной нулю второй производной на всей области определения сплайна. При максимальной точности сплайн становится интерполирующим, то есть проходит строго через все точки. В промежутке от минимальной до максимальной точности параметр сглаживания меняется непрерывно, позволяя найти оптимальную степень сглаживания.

Итак, сплайны действительно являются подходящим классом функций, в точности удовлетворяющим выдвинутым требованиям.

Выбранный нами вид сглаживающих сплайнов [см. 2, 4] минимизирует усредненный квадрат второй производной по всей области определения функции:

(13)

Кроме того, выполняется ограничение на отклонение сплайна от эмпирически заданных точек:

(14)

Здесь квадраты отклонений взвешиваются на количество точек в интервале i, поскольку точность определения значений f_i обратно пропорциональна корню из N_i:

(15)

Если мы зададим в ограничении (14) равной остаточной дисперсии для случая линейной регрессии , то сплайн выродится в линейную функцию от z. Если задать равным нулю, то сплайн станет интерполирующим и будет проходить через все эмпирические точки f_i.

Для удобства параметризации степени сглаживания вместо будем использовать безразмерный параметр точности :

(16)

При уменьшении от 1 до ½ возрастает от 0 до . Таким образом, задает точность аппроксимации, нормированную на единицу. Точность, равная единице, будет означать абсолютную точность. Точность, равная ½, будет означать точность линейного приближения. Точность меньше ½ не будет приводить к дальнейшему огрублению приближения, если пользоваться тем же алгоритмом. Для обобщения мы искусственно продолжим эту зависимость. Что может быть грубее линейной зависимости? Естественно, только отсутствие всякой зависимости, то есть константа. Тогда точность между ½ и 0 будет соответствовать переходу от линейного приближения к среднему значению f:

(17)

Имеет смысл дополнить область изменения еще одним значением: -1. Этому значению можно сопоставить отсутствие не только изменений в распределении, но и фактически отсутствие самого распределения. Для параметров Бета-распределения это означает их равенство единице, при котором распределение вырождается в равномерное.

Изменение кривой, аппроксимирующей зависимость a(z), при изменении параметра точности от -1 до 1 можно видеть на следующем рисунке:

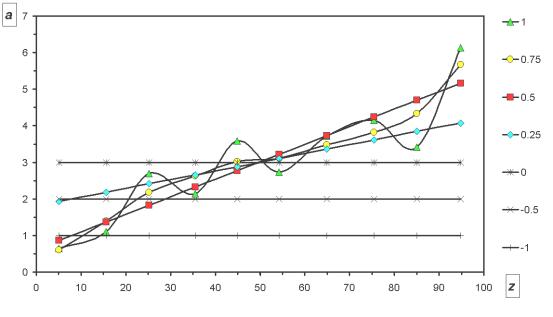
Рисунок 4. Восстановление a(z) с разной точностью аппроксимации.

В фазовом пространстве {a,b} это же будет выглядеть так:

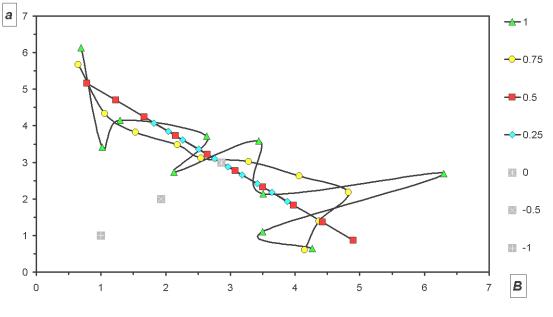
Рисунок 5. Восстановление {a(z), b(z)} с разной точностью аппроксимации.

Определив вид функции, которая может аппроксимировать параметры распределения с контролируемой точностью, остается найти критерий, который позволит определить оптимальное значение точности.

Выбор оптимальной степени сглаживания

Отклонения параметров a_i и b_i от теоретических значений a(z_i) и b(z_i) имеют стохастическую природу, то есть вызваны случайным характером формирования выборки. Гипотеза о том, что эти отклонения действительно случайны, а не носят систематический характер, поддается проверке. В математической статистике хорошо известен непараметрический критерий Колмогорова-Смирнова, который позволяет проверить гипотезу о случайности отклонения эмпирического распределения F_n(x) от известного теоретического F(x) на основании статистики D_n:

(18)

Чем больше значение статистики D_n, тем с меньшей вероятностью можно получить его случайно. Чтобы отвергнуть гипотезу о случайности отклонения, эта вероятность должна быть достаточно мала, меньше некоторого порога, например 5% или 0,1%. Но так поступают при сравнении единственного имеющегося у исследователя эмпирического распределения с теоретическим. Мы же имеем дело с целым набором из m эмпирических распределений (по одному на каждый интервал z_i-1-z_i, где i=1..m), каждому из которых соответствует свое теоретическое (восстановленное) распределение. Оказывается, что и в этом случае процедура принятия решения о случайности наблюдаемых отклонений в распределениях ненамного сложнее. Действительно, для этого достаточно отметить тривиальное свойство вероятности, рассчитываемой по статистике D_n. Если гипотеза о случайном отклонении эмпирических распределений имеет место, то рассчитываемая по критерию Колмогорова-Смирнова вероятность будет распределена равномерно.

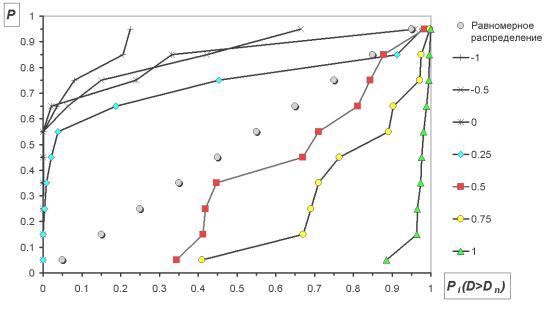
Рисунок 6. Зависимость формы распределения от точности аппроксимации.

Отсюда сразу вытекает формулировка критерия оптимальности: при наилучшем сглаживании параметров Бета-распределения наблюдается наиболее близкое к равномерному распределение вероятностей , вычисленных для всех интервалов (i) по критерию Колмогорова-Смирнова. Для определения близости этого распределения к равномерному можно еще раз использовать тот же критерий (Колмогорова-Смирнова), взяв на этот раз в качестве теоретического распределения равномерное.

Рисунок 7. Поиск оптимальной точности аппроксимации по максимальной близости распределения к равномерному.

Изменение плотности условного распределения на сетке из 10 интервалов в результате сглаживания, можно видеть на рис. 8 и 9.

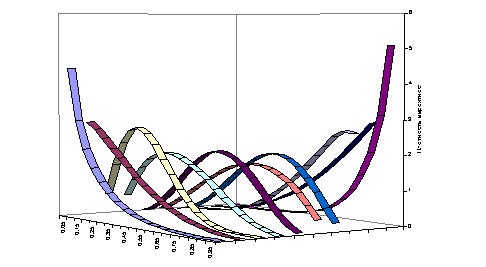
Рисунок 8. Плотность условного распределения по интервалам.

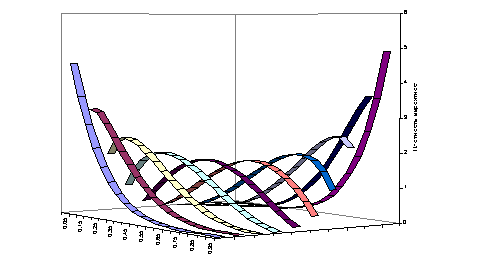
Рисунок 9. Плотность условного распределения после сглаживания.

Проверка точности восстановления Бета-распределения

Расчеты на контрольной выборке показали удовлетворительное восстановление параметров распределения при некоторых разбиениях (рис. 10). Вместе с тем обнаружилось искажение формы кривой a-b при числе интервалов меньше 10.

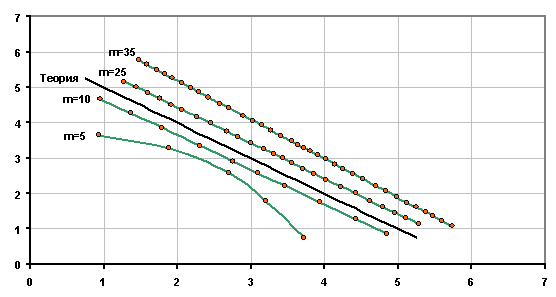Рисунок 10. Восстановление параметров Бета-распределения a и b на контрольной выборке объемом 400 наблюдений при различных разбиениях (m - число интервалов).

Этот эффект имеет простое объяснение: при малом числе интервалов каждый из них захватывает широкую область значений z, что приводит к смешению распределений внутри интервала и искусственному увеличению выборочной дисперсии . А поскольку оценки a и b обратно пропорциональны дисперсии (см. формулы 4,5), то ее увеличение приводит к уменьшению параметров распределения тем более заметному, чем более различаются смешиваемые распределения. Нами были проведены дополнительные вычислительные эксперименты, которые выделили эффект смешивания распределений внутри интервалов в чистом виде. Полученные в этих экспериментах кривые a-b дали в точности ту же картину, что на рисунке 10 при m=5.

Кроме искажения формы кривой при разбиении на малое число интервалов, наблюдается систематическое увеличение оценок параметров a и b при увеличении числа интервалов. На рисунке 11 показано, как растут средние оценки параметров (теоретическое значение равно 3.0) и разброс этих оценок относительно средних (кривая в нижней части рисунка).

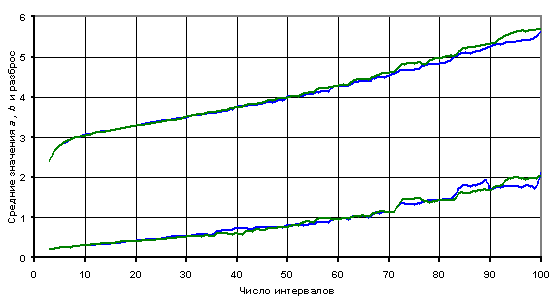Рисунок 11. Зависимость восстановленных значений a и b (сверху) и их среднеквадратичных разбросов (снизу) от числа интервалов m.

Этот эффект обусловлен тем, что при увеличении числа интервалов количество наблюдений внутри каждого из них уменьшается и разброс оценок a_i и b_i возрастает. Когда оценки рассеиваются симметрично относительно теоретического значения, систематического смещения восстановленных значений не происходит. В нашем же случае наблюдается длинный хвост справа, в результате чего усреднение дает завышенные оценки a и b, что мы и наблюдаем.

Для проверки этого предположения мы сгенерировали выборку на основе Бета-распределения с фиксированными параметрами a=0.5 и b=5.5 объемом 400 наблюдений. Имитируя разбиение выборки на 1, 2, 4 и т.д. интервалов скользящим интервалом соответствующего размера, мы получили средние оценки, которые сведены в таблице:

m	1	2	4	5	8	10	16	20	25	40	50	80	100
	0.519	0.524	0.524	0.529	0.542	0.554	0.595	0.622	0.658	0.766	0.841	1.254	1.996
	5.218	5.240	5.352	5.374	5.529	5.724	6.313	6.672	7.158	8.895	10.234	21.838	38.258
	0.0905	0.0910	0.0896	0.0900	0.0898	0.0896	0.0900	0.0906	0.0909	0.0906	0.0905	0.0905	0.0904
	0.0204	0.0206	0.0201	0.0202	0.0201	0.0200	0.0202	0.0205	0.0206	0.0205	0.0204	0.0204	0.0204

Из таблицы видно, что оценки и существенно отличаются от исходных, начиная уже с m=10.

В то же время, оценки и не зависят от разбиения и восстановленные по ним a и b также не должны от него зависеть. Тем не менее, алгоритмическая реализация такого подхода является нетривиальной задачей и требует дополнительной проработки, что предполагается осуществить в ходе дальнейшего развития метода.

Определение минимального объема выборки

Если представить себе последовательный ряд выборок постепенно уменьшающегося объема от бесконечного количества до одного наблюдения, нетрудно увидеть, что к концу этого ряда мы полностью теряем какую бы то ни было информацию о распределении в генеральной совокупности. Но нам хотелось бы более точно определить границу, до которой еще возможно восстановить исходное распределение. Для этого мы должны найти критерий, позволяющий отличить ситуацию, в которой исходное распределение восстановлено, от той, в которой оно не восстановлено или восстановлено неверно. Если такой критерий будет статистическим, то его результат должен носить вероятностный характер, то есть он позволит нам рассчитать вероятность восстановления распределения. Мы можем задать порог, например 95%, ниже которого будем считать, что качество восстановления теоретического распределения нас уже не может устроить. Объем выборки, при котором последний раз достигается этот порог, будем считать минимальным.

Понятно, что минимальный объем выборки не есть фиксированное число, а зависит от самого теоретического распределения - масштаба a и b и характера их изменения. Так что, учитывая многомерность задачи, в данной работе мы сможем определить минимальный объем выборки только для распределений самых простейших видов.

Но, несмотря на невозможность заранее указать, какой минимальный объем выборки необходим в каждом конкретном случае, все же существует способ примерно оценить его по реальным данным. Этот способ состоит в том, что мы принимаем восстановленное распределение за теоретическое и для него запускаем процедуру определения минимального объема выборки. Таким образом нам удастся учесть масштаб и особенности изменения параметров распределения для конкретных данных. Правда, стоит заметить, что восстановленное распределение не должно быть равномерным, иначе не будет работать критерий восстановления распределения.

Указанный способ определения минимального объема выборки легко трансформируется в стратегию точного изучения распределения. Для этого достаточно применять его итерационно: получив на очередном шаге некоторое приближение к функции распределения, по нему определяем минимальный объем выборки, закладывая в критерий все более и более жесткий порог вероятности восстановления распределения. На каждом следующем шаге, увеличивая объем выборки до расчетного, мы получаем все более точные восстановленные распределения, достигая в пределе цель исследования в виде точной теоретической модели условного распределения.

Теперь перейдем к формулировке самого критерия восстановления распределения. Чтобы построить такой критерий, мы должны уметь сравнивать восстановленное распределение с теоретическим. Одна такая мера расстояния между распределениями нам уже известна (18). Значит, мы всегда в состоянии определить, к какому распределению ближе восстановленное - к теоретическому или к равномерному. Далее, мы можем провести достаточное количество численных экспериментов с генерацией выборок заданного объема и определить процент случаев, в которых восстановленное распределение оказывается ближе к теоретическому, чем к равномерному. Этот процент случаев и будет оценкой искомой вероятности восстановления распределения по выборке заданного объема.

Литература

1. Ростовцев П.С. Бета-анализ иерархии социально-экономических объектов // Регион: экономика и социология. - , 2001. - N4. - C.121-138.

2. Морозов B.A. O задаче дифференцирования и некоторых алгоритмах приближения экспериментальной информации, в сб. "Вычислительные методы и программирование", 1970, вып.ХIV, Изд - во МГУ, 46 - 62.

3. Носач В.В. Решение задач аппроксимации с помощью персональных компьютеров. - М: МИКАП, 1994. - 382 с.

4. БЧА НИВЦ МГУ. IS01R. Сплайн-сглаживание (Текст подпрограммы построения одномерного сглаживающего кубического сплайна на языках Фортран и C++). http://www.srcc.msu.su/num_anal/lib_na/cat/i/is01r.htm Ссылка действительна на 09.12.2002