Ростовцев П.С., Костин В.С., Жданов А.С.

Автоматизация типологического группирования: две модели однородности.

Исследование поддержано грантами РФФИ 00-06-80221 и 01-06-06005

Аннотация

Понятие типологической группировка объединяет логику группирования и цель группирования - получение однородных групп объектов. В работе рассматривается метод автоматизации типологического группирования на основе эмпирических данных, реализующий два критерия однородности. Первый критерий однородности основан на модели многомерного дисперсионного анализа, обобщенного для неколичественных данных. Второй - связан с моделью регрессионного анализа: распределение данных в типах описывается различными регрессионными зависимостями. Автоматизация группирования основана на множественных сравнениях значимости вариантов группирования, в которых активно используется статистические эксперименты.

Введение

По определению, которое дается в общей статистике, типологией называется логическое разделение совокупности объектов на качественно различные группы объектов - типы.

Проблема построения типологии возникает в задачах

- классификации регионов по остроте экономических проблем;

- анализе текучести кадров в промышленности;

- исследовании образа жизни населения;

- выявления политических платформ населения в анализе электорального поведения;

- сегментации рынка в маркетинговых исследованиях;

- выявления групп риска в медицине;

- во многих других задачах.

Построение типологии обычно является трудоемкой задачей, требующей тщательного изучения теоретического материала и эмпирических данных. Традиционно наиболее распространенным способом построения типологий на основе эмпирических данных в настоящее время является теоретическое формулирование типов, конструирование этих типологий в виде вторичных переменных средствами преобразования данных статистических пакетов и проверка качества типологии. Для этого необходимы многоплановые исследования связей разного типа переменных и множественные сравнения групп объектов на основе разнообразных критериев однородности. Для такого анализа необходимы как известные программные средства, включенные в статистические пакеты, так и специальное математическое обеспечение. Полное рассмотрение проблемы требует рассмотрения философских аспектов, вспомогательных средств и непосредственно автоматизации типологического анализа.

Методическим вопросам типологического анализа значительное внимание уделено как зарубежными авторами, так и в отечественной литературе [21, 22, 26].

Автоматизация типологического группирования передает компьютеру часть работы, связанную с множественными сравнениями вариантов группирования. Множественные сравнения опасны высокой вероятностью выбора варианта группирования, связанного со случайными отклонениями в данных.

В данной работе мы ограничимся описанием метода и программного обеспечения непосредственного конструирования типологической группировки, разработанного коллективом авторов. Одним из ключевых моментов здесь является решение проблемы множественных сравнений.

В определении типологии неявным образом присутствуют два элемента. Во-первых, это наличие критерия однородности. При анализе эмпирических данных такой критерий формулируется на основе соответствующих переменных. Вторым элементом логики группирования является логика группирования. Естественным подходом для формализации типологического группирования, поэтому, является использование в качестве критерия однородности внутригруппового разброса целевой переменной или, что равносильно, межгруппового разброса - как характеристики различия типов. Еще одним типом однородности является подчинение объектов типа одной модели зависимости, например регрессионной. В качестве логики группирования естественно использовать интервалирование и группирование значений переменных в сочетании с комбинированием их значений. Теоретическая основа такого подхода рассмотрена, в частности, И.И. Елисеевой и Е.О. Рукавишниковым [7] при исследовании типологического группирования методом комбинационных группировок.

Многими отечественными и зарубежными авторами в качестве начального приближения типологии использовались результаты кластерного анализа. Здесь сложность состоит в изучении логики формирования типов. Этот подход использовался множеством отечественных и зарубежных исследователей (см. например Айвазян С.А., Мхиторян В.С. [1]Н.Г. Загоруйко [6] и др.). Вопросы адекватности этого подхода рассмотрены с методической точки зрения в работах методологического отдела Института социальных исследований РАН Г.Г.Татаровой и Ю.Н.Толстовой [21,22].

Близки к решению этой задачи дискриминантный анализ [2], а также методы построения логических решающих правил (подходы, развиваемые Г.С.Лбовым и Н.Г.Старцевой [8,9], за рубежом - Ф.Меллером и В.Капекки [12], метод Chaid в статистическом пакете SPSS [27] и др.). В этих методах однородность получаемых классов (по нашему определению - типов) оценивается по одной критериальной переменной. Это достаточно тяжелое ограничение,

Наиболее продвинуты в этом отношении работы В.И.Котюкова. Им сформулирован общий подход поиска бинарных логических правил для поиска классов закономерностей и в этом ключе реализован алгоритм построения решающего правила для распознавания регрессионных зависимостей [10].

Ранее авторским коллективом рассматривались и реализовались схемы получения типов, однородных в смысле дисперсии зависимых переменных [15,16]. Конструирование типологической группировки заключалась в иерархическом группировании совокупности объектов по переменным X. Ее оптимизация состоит в максимизации Q(R,Y). В качестве Q(R,Y) использовалась сумма коэффициентов детерминации для количественных Y и коэффициентов Валлиса для неколичественных Y.

Хотя в предложенных методах и программном обеспечении исследовалась устойчивость получаемых классификаций (типологий), методы оставались скорее описательным, поскольку в нем не использовался критерий значимости. Лишь алгоритм Chaid [27] реализует этот критерий, однако используемый им метод множественных сравнений Бонферрони достаточно груб и не учитывает связи между статистиками тестов.

Между тем проблема множественной оценки значимости в типологическом группировании стоит в полном объеме, поскольку при построении эмпирической типологии нужно исследователем сравнивается множество альтернатив группирования. Особенно это касается автоматизированных процедур выбора группировки.

Реально в достаточно сложных ситуациях множественные сравнения можно провести только с помощью компьютерных экспериментов, а до настоящего времени мощности компьютеров для решения многих задач было достаточно лишь для достаточно простых задач.

Буквально в течение ближайших 3 лет производительность техники возросла настолько, чтобы осуществить идею типологического анализа на основе экспериментально-статистического анализа множественных сравнений, тем более что это обеспечено развитием методов Монте-Карло [5] и Bootstrap [25]. Прежде всего, это идея была реализована в макетной программе детерминационного и типологического анализа [17]. Позднее она была воплощена в математическое обеспечение анализа таблиц для неальтернативных вопросов [16], а также в программе детерминации моделей DAMO [20]. Впрочем, детерминационный анализ, основанный на простых статистиках, возник значительно раньше [19].

В данной работе мы рассматриваем метод автоматизации типологического группирования, основанный на множественных сравнениях. Рассматриваются две модели однородности типов: модель однородности, заимствованная из дисперсионного анализа, связанная с максимизацией межгруппового разброса средних [2], и модель объяснения различия между регрессионными уравнениями, которая ранее была использована И.И.Елисеевой и В.О.Рукавишниковым [7] и В.И.Котюковым [10]. Оказалось, что использование остаточной дисперсии в алгоритме позволяет использовать для целей типологического группирования один и тот же алгоритм.

Опыт разработки и использования собственных процедур автоматизации типологического группирования, а также применение известного математического обеспечения, такого как Answer Tree (современное название программы CHAID), показал неустойчивость конструирования группировки. Содержательно, эта неустойчивость обусловлена наличием многих путей построения группировки, а формально - обычным наличием нескольких переменных, дающих почти одинаковое качество группирования. Поэтому программа автоматического группирования, беря на себя основную рутинную работу, должна позволять исследователю вмешаться в процесс построения практически в любой момент и проверить качество группирования не только по предложенным формальным показателям, но и другими средствами. Именно на такой подход ориентирована представленная в статье программная реализация метода.

Вклад авторов: основная идея метода принадлежит П.С.Ростовцеву, В.С.Костин написал программу, реализующую метод в целом. Алгоритмы одномерного группирования, осушествляемые на шаге группирования написаны им совместно с А.С.Ждановым.

Типологическое группирование: однородность и различие типов

Для автоматизации типологического группирования мы пользуемся рабочей формулой:

Типология = Логика Группирования + Цель Группирования

Логику группирования мы осуществляем, конструируя классификацию объектов R={R₁,…,R_m} из множества «независимых» переменных X={X₁,…,X_k} .

Цель группирования связана с определением модели однородности классов объектов (типов).

Предположим вначале, для простоты, что у нас имеется единственная переменная X.

В данной работе мы рассматриваем две модели однородности.

1. Модель объясненной дисперсии. Имеется множество зависимых переменных Y₁,…,Y_t. (количественных или неколичественных). Задача получить разбиение совокупности на качественно различные по Y группы объектов R={R₁, …, R_m}, классы которого описываются в терминах X. Критерий - , где - доля объясненной дисперсии (коэффициент детерминации или коэффициент Валлиса для количественных или номинальных Y соответственно), g - число целевых переменных Y. В случае количественных переменных величина h(Y/R) выражается через смещенную оценку дисперсии Y и средние Y в классах R:

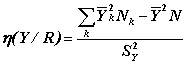
где N_k - число объектов в классе R_k, а N общее число объектов в анализируемой совокупности.

Коэффициент Валлиса сводится к аналогичной формуле благодаря представлению Y в виде совокупности дихотомических переменных Y(t) 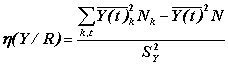, где t соответствует значению t переменной Y, а .

Критерий отражает различие средних в классах R.

Следует заметить, что предварительное центрирование переменных Y и Y(t) и нормирование делением их на S_Y дает показатель Q(R) вида , где символом U обозначены стандартизованные переменные. Такое представление целевой функции в значительной степени упрощает вычисления. Кроме того, здесь весьма несложно учесть пропуски в данных, подставив в данной формуле N_k=N_k(U) - число валидных по переменной U объектов в классе R_k.

Для вычисления критерия для каждого значения X накапливаются суммы значений стандартизованных целевых переменных U на основании которых вычисляются значения для каждого R_k вычисляются значения , а затем и сам критерий.

2. Модель регрессии: имеется зависимая переменная Y и независимые переменные Z₁,…,Z_m. Цель - найти разбиение R, между классами которого наблюдается существенное различие регрессий. Критерий - .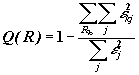

Здесь e_ij - регрессионный остаток на j- м объекте i-го класса, а e_j - регрессионный остаток, полученный на совокупности данных в целом.

Таким образом, во второй модели однородность типа определяется моделью взаимосвязи между переменной Y и независимыми переменными Z₁,…,Z_m.

Известно, что вектор коэффициентов регрессии B находится по формуле B=(Z^TZ)^-1Z^TY, где Z - матрица данных по независимым переменным, а символ ^T - означает ее транспонирование. Метод Холецкого [13] при нахождении коэффициентов регрессии по этой формуле позволяет одновременно найти и сумму квадратов остатков, необходимую для вычисления нашего критерия.

Для вычисления критерия здесь необходимо вычислить суммы произведений Z^TZ, Z^TY, Y^TY каждого значения X, на основании которых вычисляются составляющие критерия для каждого R_k, а затем и сам критерий.

Для фиксированного числа классов критерий оптимизируется варьированием границ интервалов разбиения R, если X - ранговая переменная. Оба критерия аддитивны, поэтому в этом случае реализуется точный алгоритм на основе метода динамического программирования [3]. В случае номинальной переменной X оптимизация происходит перемещением объектов из класса в класс (локальный алгоритм).

Указанные критерии используются не непосредственно, а служат для определения критерия значимости - вероятности случайно получить "лучший" результат. Но прежде, чем рассматривать критерий значимости мы опишем алгоритм типологического группирования в целом.

Алгоритм типологического группирования.

Если множество X состоит из единственной переменной (), конструируется одномерная типология. Построение типологии состоит в оптимальном интервалировании ранговых, количественных переменных или объединении в произвольном порядке значений номинальных переменных.

В многомерном группировании многократно используются одномерное группирование, в котором . Такое группирование происходит в два этапа.

Первый этап, анализ, состоит в последовательном группировании совокупности объектов по признакам.

Прежде всего, по каждому из "независимых" признаков ищется оптимальная с точки зрения критерия значимости группировка объектов; "лучшая" среди этих группировок берется в качестве начального приближения типологии . На следующем шаге выбирается "оптимальная" с точки зрения значимости пара (класс полученного разбиения, переменная), по которой происходит группировка объектов этого класса. При определении значимости пары (класс полученного разбиения, переменная) каждый класс рассматривается независимо и для него рассматривается своя задача оптимального группирования.

В результате разбиения указанного класса по соответствующему признаку получается группировка R¹. На следующих шагах процедура повторяется, получаются классификации R², R³, … и т.д. Процесс идет до тех пор, пока исследователь не решит, что полученный результат удовлетворяет полнотой описания связи X и Y, либо очередной шаг дает незначимое значение критерия. Впрочем, уровень значимости, на котором следует прекратить конструирование типологии также определяется исследователем использующим метод.

Таким образом, в ходе последовательного разбиения получаются максимально внутренне однородные группы.

Второй этап состоит в синтезе типов - объединении классов полученной классификации в заданное число классов.

Значимость в одномерном группировании

С точки зрения использования критерия Q(R) наилучший результат в модели объясненной дисперсии должен получиться в случае, когда в качестве переменной X используется порядковый номер объекта, а разбиение R совпадает с X. Похоже обстоят дела в регрессионной модели. Такой результат бессмыслен со всех точек зрения. Поэтому при конкуренции между переменными X и/или группировками по X с разным числом классов, вместо Q(R) мы используем в качестве критерия наблюдаемую значимость Q(R) - вероятность случайно получить Q(R) больше, чем выборочное значение Q^выб(R) на a^выб=P{Q^выб(R)<Q(R)}.

Таким образом, шкала значений Q(R) заменяется на шкалу значимости. Традиционно эта шкала имеет обратный порядок: чем меньше значение a^выб, тем ценнее результат. Сложный алгоритм вычисления оптимального значения Q(R) не позволяет воспользоваться для вычисления наблюдаемой значимости стандартными статистиками и распределениями Фишера и хи-квадрат. Поэтому мы вынуждены прибегнуть к статистическому эксперименту.

Для вычисления a^выб в качестве модели случайных данных взята модель отсутствия связи между переменными модели однородности (Y в модели объясненной дисперсии; Y и Z - в модели регрессии) и группировочными переменными X.

Для оценки a^выб производятся эксперименты по случайному перемешиванию в таблице данных значений переменных X. При этом, в каждом из заранее заданного числа n_exp экспериментов получается случайное значение критерия Q_j=Q(R) (j=1,…,n_exp), оптимальное для сгенерированных случайных данных. Естественно, разбиение R=R(j) оказывается в каждом эксперименте - случайным, поскольку оно получается на после перемешивания значений X.

Значения Q_j вместе с выборочным значением Q^выб(R) можно расположить в виде вариационного ряда Q₍₁₎ £ Q₍₂₎ £ … £ £ Q^выб(R) £ £ … £ . Если значение Q^выб(R) не превышает max(Q_j)=, то a^выб можно оценить непосредственно по выборке (оценка a^выб=r_выб/(n_exp+1). Зачастую это практически невозможно. Поэтому в данной работе мы аппроксимируем распределение Q(R) бета распределением. Основанием для использования такой аппроксимации послужили результаты исследования алгоритма кластерного анализа на одно-кластерной структуре, в котором многочисленные статистические эксперименты показали незначимое отличие распределения Q(R) от бета распределения, а также успешное использование ее в нашем методе детерминации моделей.

Известно, что бета распределение связано с распределениями Фишера, биномиальным, гамма распределением, равномерным и весьма гибко меняет форму, связанную всего с двумя параметрами [23]. Безусловно, сделанный нами выбор класса распределений – эвристика, однако опыт показывает – это неплохая эвристика. В дальнейшем она может быть уточнена и в большей степени обоснована.

Оценки параметров бета распределения a и b вычисляются на основе оценок матожидания и дисперсии полученной выборки {Q_j}. После этого не составляет проблемы вычислить a^выб=1-B(Q^выб,a,b), где a=a(R) и b=b(R), а B(Q^выб,a,b) значение функции оцененного бета распределения в точке Q^выб.

Каждому случайному наблюдению Q_i на основании его ранга r_i можно также приписать значимость r_i/(n_exp+1), однако лучше использовать ее сглаженные оценки 1-B(Q_j,a,b).

Более того, с помощью бета распределения можно оценить качество разбиения, которое сформулировано самим исследователем после модификации выданного компьютером варианта группирования R: a=1-B(Q(R),a,b). Это и есть возможность вмешательства исследователя в процесс формирования типологии на этапе одномерного группирования.

Конкуренция разбиений и множественная значимость разбиения группы объектов

В действительности имеется множество переменных, по которым может быть разбита совокупность. Кроме того, имеется возможность варьировать числом классов разбиения каждой переменной. Для оптимального разбиения вершины мы должны перебрать все эти варианты.

Обозначим R¹,…,R^r варианты такого разбиения. Каждый из вариантов имеет свой наблюдаемый уровень значимости a_i, определяемый на основе множества n_exp перемешиваний (рис.1). При этом по формуле a_ij=1-B(Q_ij,a_i,b_i) вычисляются "гладкие" оценки значимостей Q_ij, чем r_ij/(n_exp+1), получаемых в экспериментах (таблица 1).

Целесообразно в качестве оптимального разбиения взять разбиение Rⁱ , полученное из переменной X_i, с наименьшим наблюдаемым уровнем значимости (min ). Из-за множественных сравнений уровень значимости a_i не несет должной информации о качестве выбранного разбиения - перебором случайных значений мы также можем достигнуть малых значений a_i, которые ошибочно можем принять за свидетельство обнаруженных закономерностей. Для того, чтобы сделать правильный вывод о значимости шага разбиения следует изучить распределение _.

Таблица 1. Значимости вместо значения Q_ij и оценка теоретического распределения mina_i.

Разбиение	Эксперименты					A	b	Оценка значимости
	1	…	j	…	nexp
R^1	Q11	…	Q1j	…		a1	b1	a1=B(Q1,выб,a1,b1)
…	…	…	…	…	…	…	…	…
R^i	Qi1	…	Qij	…		ai	bi	ai=B(Qi,выб,ai,bi)
…	…	…	…	…	…	…	…	…
R^r	Qn1	…	Qnj	…		ar	br	ar=B(Qr,выб,ar,br)
min a	aM1		aMj		aMnexp	aM	bM	aM=B(ai,aM,bM),(ai-min)

Для оценки этого распределения используются наблюдаемые в экспериментах значения минимумов a_Mj=_. Для них также оцениваются параметры a_M и b_M бета-распределения. После чего наблюдаемая множественная значимость разбиения Rⁱ вычисляется по формуле a_M=B(a_i,a_M,b_M).

Если Rⁱ выбрано в качестве разбиения вершины, a_M=B(a_i,a_M,b_M) является также значимостью вершины.

Оценка множественной значимости модифицированного разбиения

Автоматическое построение классификации во многом зависит от появления случайных объектов, не вписывающихся в общую тенденцию. При группировании значений X возможно случайное отнесение этих значений к тому или иному классу R, поскольку случайные отклонения совместных распределений переменных X и целевых переменных, определяющих модели, могут несколько искажать общую тенденцию. Поэтому, в ущерб формальным характеристикам критерия Q и его значимости целесообразна модификация разбиений (изменение границ интервалов или перенесение групп объектов из класса в класс для номинальных X). На шаге разбиения с этой целью возможна также замена оптимального Rⁱ на некоторое, может быть модифицированное, разбиение R^l. Построенная шкала значимости

a_M=B(1-B(Q_l,выб,a_l,b_l),a_M,b_M)

позволяет оценить, насколько модифицированное разбиение может заменить "оптимальное", отобранное по формальным критериям.

Таким образом, это следующая возможность вмешательства в процесс построения типологии, уже на этапе конкуренции переменных.

Верхняя оценка значимости этапа анализа в построении типологии в целом.

К сожалению, точная оценка значимости типологии в целом на настоящий момент практически невозможна. Однако никто не мешает нам здесь воспользоваться известным методом Бонферрони.

Основное соотношение Бонферрони состоит том, что вероятность хотя бы одного отклонения гипотезы из множества гипотез не превышает суммы этих вероятностей для отдельных гипотез [11].

Поэтому верхняя граница значимости - вероятности принять за существенную неоднородность случайное ее проявление при разбиении хотя бы одной вершины - оценивается простой суммой выборочных значимостей вершин.

О синтезе типов

Синтез типов (объединение вершин дерева в заданное число типов) останется скорее не статистической, а описательной процедурой, поскольку в настоящий момент, по всей вероятности, невозможно сколько-нибудь серьезно оценить распределение критерия Q(R), полученного столь сложным путем.

Иллюстративный пример

Модель объясненной дисперсии достаточно ясна для понимания - вполне естественно стремиться получить группы объектов, существенно различающиеся по средним значениям некоторых показателей или по распределению номинальных переменных. Поэтому мы посвятим данный раздел выявлению групп объектов, различающихся регрессионной зависимостью. Гипотеза состояла во влиянии на эту взаимосвязь размера семьи и уровня ее благосостояния.

Для нашего вычислительного эксперимента использовались часть данных Российского мониторинга экономики и здоровья населения (RLMS) [14]: выборка 1996 г. по городским домашним хозяйствам (2604 семей состоящих не менее, чем из двух членов, переменные - жилая площадь, денежные доходы населения, число членов семьи, сделанные в течение одной недели закупки молочных продуктов, спиртного и табака, сладостей, наличие автомобиля). Из 2600 объектов 395 было отброшено из-за неопределенности данных по жилплощади и доходам. Для снятия инфляционных эффектов душевой доход ранее был приведен безразмерным единицам - "промедианному доходу" - для каждой семьи душевой доход исчислялся в числе медиан дохода по всей выборке [4].

Непосредственное использование дохода и жилплощади в регрессионных уравнениях неудобно ввиду скошенности распределения этих показателей. Опыт показывает, что их логарифмирование достаточно хорошо исправляют эту ситуацию. Таким образом, в качестве зависимой переменной в уравнении регрессии использовался натуральный логарифм полезной жилой площади (LNSQ), приходящейся на одного члена семьи, а в качестве предиктора - натуральный логарифм промедианного денежного душевого дохода (LINCOME).

Претендовали на участие в построении типологии переменные "число членов семьи" (MEMB) и переменные, характеризующие благосостояние семьи: наличие автомобиля (CAR), а также характеристики разнообразия покупок: число видов молочных продуктов (MILK; виды молочных продуктов: сыр, сметана, молоко и др.), число видов сладостей (SWEET; виды сладостей: мед, конфеты, печенье и др), число видов спиртных напитков и табачных изделий (ALK; их вид взято грубо: любое вино, водка, пиво, и табачные изделия рассматривается как один вид).

Дерево группирования, полученное с помощью нашего алгоритма представлено на рис. 1. Рассмотрим, как оно было получено.

Первый шаг, как описано выше, состоял в выборе начального разбиения. После проведения 100 экспериментов наиболее существенную множественную значимость (8.72E-258) показала группировка по числу членов семьи в 3 классе (см. таблицу 2): малые семьи, средние семьи и большие семьи.

Таблица 2. Выбор переменной для первого шага разбиения. Фрагмент таблицы значимостей.

Переменная	Название переменной	Тип	Число классов	Значимость	Множественная значимость	Критерий
MEMB	Число членов семьи	R	2	9.86E-210	7.54E-209	0.2909
MEMB	Число членов семьи	R	3	8.72E-258	6.67E-257	0.3843
MEMB	Число членов семьи	R	4	2.9E-255	2.22E-254	0.3979
CAR	Легковой автомобиль	N	2	0.79	0.99	0.0002
MILK	Видов молочных изд.	R	2	0.000000775	0.00000593	0.0134
MILK	Видов молочных изд.	R	3	0.000000108	0.000000826	0.0214
…	…	…	…	…	…	…

Далее алгоритм показывал, что дальнейшее разбиение опять следует вести по числу членов семьи, но с содержательной точки зрения такая типология была бы неинтересна. Поэтому мы использовали преимущество интерактивности и провели два разбиения малых семей по наличию автомобиля. Хотя множественная значимость разбиения на средних семей на 2 более мелкие группы оказалась равна 0.000000000278, мы разбили эту группу по признаку наличия автомобиля (множественная наблюдаемая значимость 0.00237). Точно также, можно было разбить малые семьи по переменной ALK на 5 групп (множественная значимость 0.00486), но это неприемлемо с точки зрения обозримого описания группировки. Поэтому мы использовали разбиение это группы по переменной CAR (значимость 0.0114). Остальные разбиения оказались также неприемлемыми из содержательных соображений или из формальных, поскольку были незначимы.

Итак, получились группы

- малые семьи, владеющие автомобилем;

- малые семьи, не имеющие автомобиля;

- средние семьи, владеющие автомобилем;

- средние семьи, не имеющие автомобиля;

- большие семьи.

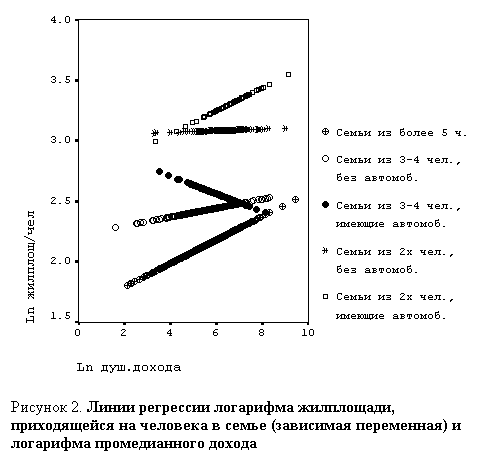
Различие регрессионных зависимостей в этих группах нагляднее всего представляется рисунком 2. В силу множества сравнений при конструировании типологии значимость коэффициентов регрессии в таблице 3 имеет описательный характер.

Таблица 3. Коэффициенты регрессионных уравнений в полученных группах.

		B	T	Значимость
Малые семьи, имеющие автомобиль	Константа	2.6709	9.1889	0.0000
	LINCOM логарифм душевого дохода	0.0959	2.2108	0.0309
Малые семьи без автомобиля	Константа	3.0400	13.2445	0.0000
	LINCOM логарифм душевого дохода	0.0070	0.1904	0.8492
Средние семьи, имеющие автомобиль	Константа	3.0007	14.8672	0.0000
	LINCOM логарифм душевого дохода	-0.0734	-2.1664	0.0319
Средние семьи без автомобиля	Константа	2.2212	22.1552	0.0000
	LINCOM логарифм душевого дохода	0.0370	2.0106	0.0447
Большие семьи	Константа	1.5976	24.3943	0.0000
	LINCOM логарифм душевого дохода	0.0973	8.3642	0.0000

Не проводя подробного исследования, а лишь высказывая некоторые гипотезы, скажем несколько слов о полученных группах.

Малые семьи, предположительно должны составлять, преимущественно, старшее поколение, которое покинула "оперившаяся "молодежь". За время жизни ими была заработана достаточно большая жилплощадь, поэтому линии регрессии этих групп находятся достаточно высоко.

В малых семьях, владеющих автомобилем, обнаруживается явная связь между доходами и жилплощадью. По-видимому, эти семьи достаточно активны и эта активность появляется совместно в увеличении доходов и жилплощади.

В малых семьях без автомобиля соответствующая связь отсутствует. Вероятно, в этих семьях нет средств и активности для наращивания жилой площади за счет денежных доходов. Поэтому здесь практически отсутствует связь между доходами и жилплощадью.

Удивительно, в средних семьях, владеющих автомобилями, обнаруживается обратная тенденция: чем больше доходы, тем меньше жилплощадь. Может быть это молодежь, только начинающая зарабатывать на деньги, и малая жилплощадь здесь является стимулом для зарабатывания денег, а автомобиль - средством для этого?

Средние семьи без автомобиля показывают естественную тенденцию, правда не очень значимо.

Точно такая же тенденция в больших семьях, но на более низком уровне: в этих семьях квартиры делятся на большее число членов семьи.

Оптимальное группирование полученных групп оказалось в некотором роде "вырожденным", поскольку совпадало с первым уровнем разбиения. Поэтому в данном случае синтеза типов мы не демонстрируем.

Заключение

Мы рассмотрели пока лишь только 2 модели однородности типов. Но эти модели покрывают большой пласт содержательных задач, с которыми сталкивается социолог, экономист, психолог, специалист по маркетингу и др. В дальнейшем предполагается расширить круг закономерностей, обнаруживаемых данными методами. Но более серьезной задачей в настоящее время является разработка полноценной методики применения разработанного аппарата анализа данных.

Еще одной проблемой в данной работе является проблема устойчивости результатов. В этом направлении у нас имеется определенное решение: получение доверительных интервалов оценки значимости, но, чтобы не перегружать статью дополнительными выкладками, мы пока опустили этот материал.

Программа, реализующая метод, на момент выпуска данной публикации находится в состоянии промышленной опрабации. Мы надеемся на скорейшее продвижение ее непосредственно нашему пользователю.

Литература

1. Айвазян С.А., Мхиторян В.С. Прикладная статистика и основы эконометрики. -М.: Издательство "Юнити", -1998. Стр. 452-514.

2. Аренс Х., Лейтер Ю. Многомерный дисперсионный анализ. - М.: Финансы и статистика, 1985. 230 стр.

3. Бородкин С.М. Оптимальная группировка взаимосвязанных упорядоченных объектов // Автоматика и телемеханика/ 1980. с165-172.

4. Богомолова Т.Ю., Тапилина В.С., Ростовцев П.С. Роль мобильности по доходам в изменении неравенства в распределении доходов// Новосибирск, -2001, 75 с.

5. Ермаков С.М., Михайлов Г.А. Статистическое моделирование. М., Наука, 1982.

6. Загоруйко Н.Г. Методы распознавания и их применение. - М.: Сов. радио, 1972, - 206 стр.

7. Елисеева И.И. и Рукавишников В.О. Группировка, корреляция, распознавание образов. - М.: Статистика, 1977. - 128 стр.

8. Лбов Г.С. Методы обработки разнотипных экспериментальных данных/ Новосибирск: Наука, 1981. 1983.

9. Лбов Г.С., Старцева Н.Г. Логические решающие функции и вопросы статистической устойчивости решений. - Новосибирск: Издательство Института математики СО РАН, 1999. 212 с.

10. Котюков В.И. Многофакторные кусочно-линейные модели. -М.: "Финансы и статистика" -1984. 216 с.

11. Клейнен Дж. Статистические методы в имитационном моделировании. Выпуск 2 /М.: Статистика, 1978. стр. 169-217

12. Меллер Ф., Капекки В. Роль энтропии в номинальной классификации. - в кн.: Математика в социологии. М.: "Мир", - 1977. Стр.301 - 338.

13. Мейдональдс Дж. Вычислительные алгоритмы в прикладной статистике. - М.: Финансы и статистика, 1988. 350 стр.

14. Российской мониторинг экономического положения и здоровья населения. Мир России. 1999. № 3

15. Ростовцев П.С., Костин В.С. Автоматизация типологического группирования // Препринт 137, ИЭиОПП СО РАН, Новосибирск, 1995

16. Ростовцев П.С., Костин В.С., Корнюхин Ю.Г., Смирнова Н.Ю. Анализ структур социологических данных и их устойчивости. В монографии «Социальная траектория реформируемой России. Исследования новосибирской экономико-социологической школы. Новосибирск, Наука, 1999. с. 657-677

17. Ростовцев П.С., Костин В.С., Олех А.Л. Множественные сравнения в детерминационном и типологическом анализе. // Анализ и моделирование экономических процессов переходного периода в России. Выпуск 3.- Новосибирск, ИЭиОПП СО РАН, 1998. с.209-222

18. Ростовцев П.С., Костин В.С., Олех А.Л. Множественные сравнения в таблицах для неальтернативных вопросов// Анализ и моделирование экономических процессов переходного периода в России. Выпуск 4.- Новосибирск, ИЭиОПП СО РАН, 1999. с.148-164.

19. Ростовцев П.С. Статистические характеристики детерминации/ Статистическое моделирование экономических процессов. - Новосибирск: Наука, 1991.

20. Ростовцев П.С., Костин В.С., Олех А.Л., Жданов А.С. Автоматизация анализа социально-экономических данных. Детерминация моделей // Вестник НГУ. Том 1, выпуск 1, -2000, с. 20-37.

21. Татарова Г.Г. Типологический анализ в социологии. - М.: "Наука", 1993. - 103 стр.

22. Толстова Ю.Н. Измерение в социологии

23. Хастингс Н., Пикок Дж. Справочник по статистическим распределениям – М.: Статистика, 1980.

24. Шеффе Г. Дисперсионный анализ. – М.: Наука, 1980.

25. Efron B. Better bootstrap confidence intervals.//J. Amer. Statist. Ass., 81, 1986.

26. Kluge S. Empirish begrundete Typebildung. Zur Konstruktion von Typen und Typologien in der qualitativen Socialforshung. - Bremen, Universitat Bremen. 1999, 206 s.

27. Magidson J./SPSS Inc. SPSS for Windows. CHAID. Chicago: 1993. 148 p.