П.С.Ростовцев, В.С.Костин, А.Л.Олех

Множественные сравнения в таблицах для неальтернативных вопросов

Поддержано грантом РФФИ 98-06-80150

Введение

Неальтернативные вопросы - это вопросы, предполагающие множество одновременных ответов. Например, как " Каковы Ваши жизненные ценности?", "Что тревожит Вас?", "Что Вы собираетесь купить?", "Какие лекарства Вы принимаете?". Они - постоянный атрибут социологических, психологических и других исследований, касающихся поведенческих аспектов людей. Общепринятая практика - при статистическом анализе рассматривать ответы на вопросы в виде отдельных переменных, получая по ним отдельные таблицы и другие статистические описания.

Тем не менее, информацию по этим вопросам целесообразно объединять в одну таблицу частот и других статистик. В некоторых статистических пакетах такая возможность предусмотрена (например, в системе DA [1], статистическом пакете SPSS [2]). В SPSS даже есть возможность включения в таблицы статистик по количественным переменным. Двухвходовая таблица частот по неальтернативным вопросам, по сути, представляет собой информацию о связи двух множеств дихотомических переменных, соответствующих ответам. Если присутствует суммируемая переменная, это - таблица средних и характеристик разброса в группах по сочетаниям ответов.

Наш первый опыт анализа таблиц для неальтернативных признаков [3] позволил изучать статистическую значимость связи значений, значимость отклонений средних в ячейках по отношению к итоговым средним. Проводилось также исследование структуры таблицы по различным статистикам и устойчивости этой структуры.

Наличие статистик значимости не избавляет в должной степени от случайных ошибок. Даже если все переменные независимы, в достаточно большой таблице можно получить значимые ячейки и неясно, каким порогом руководствоваться, чтобы не принять незначимые связи за значимые. Эта проблема называется проблемой множественных сравнений, она является предметом обсуждения нашей работы в отношении к двухвходовым таблицам для неальтернативных вопросов.

Прежде, чем обсуждать множественные сравнения, необходимо определить статистики, характеризующие связь дихотомических переменных и статистиками отклонений средних для количественных переменных.

Исследованию связи пары дихотомических переменных в литературе уделяется существенное внимание. Для оценки такой связи используется четырехклеточная таблица частот. Основной идеей построения мер связи является измерение сходства таблицы с таблицей, ожидаемой в условиях независимости. Такими мерами являются коэффициенты, предложенные Юлом и Эдвардсом [4], стандартизованные по моделям Пуассона и гипергеометрического распределения отклонения частот [5]. Предложенное Юлом перекрестное отношение и сейчас служит для построения лог-линейных моделей для 2-3 - мерных таблиц [6], подробный обзор мер связи имеется в книгах [7-8]. Для исследования значимости связи нам полезен подход, предложений Лерманом [9], который позволяет рассматривать как универсальную меру связи между переменными целый класс мер, полученных на основе асимптотически нормальных статистик. Этот подход полезен для одновременного использования показателей связи разнотипных переменных [10]

В таблицах для неальтернативных признаков информация по количественным переменным представляется простыми статистиками, преимущественно средними и дисперсией. При проведении дисперсионного анализа [12] ценность этой информации должна существенно возрасти. В нашем случае целесообразно рассмотреть простую схему сравнения между средним по группе, соответствующей ячейке, и средним по ее дополнению.

Хотя можно рассматривать бесконечное число статистик клеток таблиц сопряженности, следуя основным потребностям специалистов в области социальных наук, в данной работе мы ограничимся лишь статистиками смещения частот и классическим подходом к сравнению средних.

Проблема множественных сравнений возникает во многих методах, где изучается множество статистик - в регрессионном анализе, корреляционном анализе [12-13]. Эта проблема наиболее подробно рассмотрена в одномерном дисперсионном анализе. Для нас здесь наиболее интересно попарное сравнение средних в группах. При сравнении средних содержательно наиболее интересным результатом является отклонение гипотезы о равенстве математических ожиданий, поскольку это свидетельствует о взаимосвязи, о выявленной закономерности. Сравнивая множество групп, мы рискуем принять за существенные случайные отклонения.

Универсальным методом, применимым во многих областях статистического анализа является метод Бонферрони [12], суть которого состоит в следующем. Пусть проводится k сравнений и при i-м сравнении, i=1,…k, проверяется гипотеза H_i. Вообще говоря, каждая гипотеза может быть проверена по критерию значимости с заранее заданным уровнем значимости a. В случае независимых сравнений вероятность a_m отклонить хотя бы одну из гипотез H_i, в то время как все H_i верны, равна 1-(1-a)^k. При k=10 и a=0.05 величина a_m=0.40, таким образом, в 40% случаев мы будем обнаруживать ложную закономерность. Согласно методу Бонферрони, в случае множественных сравнений назначается более строгий уровень значимости для попарных сравнений. Он определяется так: задается уровень значимости для множественных сравнений a_m и в качестве попарного уровня значимости берется a=(1/k)a_m.. Так как 1-(1-a)^k<ka, в независимых сравнениях с вероятностью, меньшей a_m, ложная закономерность не будет выявлена, если все гипотезы верны. Улучшенный метод Бонферрони полагается на значимость попарных сравнений a, вычисленную решением уравнения a_m=1-(1-a)^k: a=1-(1-a_m)^1/k. В этом случае для a_m=0.05 в десяти независимых сравнениях следует брать a=0.00512.

На практике, однако, независимых сравнений нет, и этот метод дает излишне жесткие условия на обнаружение закономерностей. Тем не менее, метод замечателен тем, что применим практически в любом алгоритме статистического анализа, в частности алгоритм Chaid [14] использует его для отбора переменных для древообразного группирования данных. Имеется множество менее универсальных, но и менее грубых методов выбора значимо отличающихся средних, в частности, в статистическом пакете SPSS множественные сравнения групп представлены 14 методами.

Нами ранее были проведены исследования множественных сравнений в типологическом и детерминационном анализе [15]. В указанной работе были сформулированы основные принципы множественных сравнений на основе нескольких максимумов, а также отбора переменных и интервалов группирования данных. Данная работа является развитием полученных ранее результатов.

Свой подход к множественным сравнениям и связанные с ним рассуждения мы иллюстрируем расчетами на данных социологических исследований, проведенных отделом социальных проблем Института экономики и ОПП СО РАН.

Таблицы для неальтернативных вопросов

Начнем с рассмотрения таблицы частот.

Традиционно для исследования связи неальтернативных вопросов исследователи, наряду с частотами, изучают процентные распределение по строкам и столбцам. Ячейку таблицы для неальтернативных вопросов целесообразно рассматривать совместно с соответствующими итоговыми ячейками. Смещение процентов по сравнению с итоговыми процентами характеризуют связь в данных. Отклонения процентов не являются надежной характеристикой связи, в дальнейшем мы перейдем к статистикам значимости отклонения частот.

Нередко выборки данных оказываются смещенными, в этом случае для выравнивания выборки объектам приписывают весовые коэффициенты. В этом случае вместо частот используются суммы весов объектов. Мы будем работать преимущественно с обычными частотными таблицами, специально оговаривая случаи применения метода к "взвешенным" данным.

В качестве примера приведем фрагмент таблицы сопряженности «жизненных ценностей» и «семейного положения» (табл.1). В этой таблице "Семейное положение" - обычная номинальная переменная. Респондент может многое ценить в жизни, в частности, "Друзья", "Интересная работа" и "Семья" одновременно могут быть его ценностями, поэтому по строкам таблицы расположены ответы на неальтернативный вопрос. Соответствующие ценностям группы могут пересекаться, может быть, также, что ни одна ценность не указана респондентом, поэтому итоговые строки и столбцы в таблицах могут иметь разный смысл.

Таблица 1. Фрагмент таблицы сопряженности вопросов “Что цените в жизни?” и “Ваше семейное положение?” (частоты, проценты по горизонтали и по вертикали, средние по возрасту, стандартные отклонения, итоговые частоты – по всем объектам).

	Женат	Разведен	Вдовец	Холост	Всего
Друзья
Частота	377	39	28	69	514
%по строке	73,3%	7,6%	5,4%	13,4%	100%
%по столбцу	42,7%	44,3%	31,8%	57,0%	43,5%
Среднее	40,2	41,3	55,8	26,0	39,2
Стд.откл.	12,5	9,9	12,3	10,7	13,7
Интересная работа
Частота	342	39	24	46	451
%по строке	75,8%	8,6%	5,3%	10,2%	100%
%по столбцу	38,7%	44,3%	27,3%	38,0%	38,2%
Среднее	41,3	43,6	61,6	28,4	41,2
Стд.откл.	12,2	9,1	8,2	10,8	13,3
Семья
Частота	717	44	48	61	872
%по строке	82,2%	5,0%	5,5%	7,0%	100%
%по столбцу	81,2%	50,0%	54,5%	50,4%	73,8%
Среднее	41,1	41,3	58,4	27,4	41,2
Стд.откл.	12,8	8,6	12,8	11,3	13,6
Всего
Частота	883	88	88	121	1182
%по строке	74,7%	7,4%	7,4%	10,2%	100%
Среднее	42,5	43,1	62,4	29,4	42,8
Стд.откл.	13,3	10,4	11,3	12,8	14,7

Мы выделяем три варианта формирования частот в итоговых элементах таблицы:

1) «Всего» - это число объектов (анкет) совокупности;

2) «Всего» - это число анкет респондентов, ответивших на вопрос, по которому вычисляется распределение;

3) «Всего» - это просто сумма абсолютных частот по строке (иными словами, любой ответ здесь рассматривается как объект.

Заметим, что для альтернативных вопросов второй и третий варианты итоговых элементов эквивалентны. В соответствии с определением итоговых элементов таблицы вычисляются проценты: 1) по всем анкетам; 2)по ответившим; 3) по ответам.

Те же варианты возникают по отношению к итогам при наличии суммируемой переменной. В итоговых ячейках таблицы в зависимости от выбранного варианта расчетов размещаются средние и дисперсии 1) по всем объектам, 2) по ответившим, 3) по ответам. В последнем случае объектом наблюдения становится ответ, которому приписывается значение зависимой переменной. В принципе можно разместить и другие описательные статистики, но, чтобы не усложнять изложение мы их рассматривать не будем.

В дальнейшем, если это специально не оговорено, мы будем предполагать, что имеем дело с таблицами 1-го типа.

Статистики значимости

Как мы отметили выше, ячейка таблицы вместе с соответствующими итоговыми элементами характеризует связь между дихотомическими переменными или зависимость суммируемой переменной от сочетания значений этих переменных. Проценты в ячейке "Женат"-"Друзья" в таблице 1 практически не отличаются от маргинальных процентов, поэтому естественно заключение, что соответствующие дихотомические переменные не связаны. Однако при повторном случайном сборе данных в принципе можно получить любые смещения процентов. Статистики значимости позволяют оценить вероятность на случайных данных получить смещения, большие, чем наблюдаемые.

Z-статистика значимости отклонения частот

Для исследования значимости связи значений изучается полученная из исходной таблицы матрица частот , в которой индексы i=1 и j=1 соответствуют наличию свойств объектов, i=2 и j=2 - отсутствию свойств. Здесь N₁₁ соответствует частоте, которая содержится в исходной таблице; поскольку итоговые (маргинальные) частоты равны и , остальные ячейки этой простой таблицы восстанавливаются из N₁₁, N_1., N_.1 и N - общего итога таблицы.

В условиях независимости переменных, при фиксированных маргинальных частотах N₁₁ имеет гипергеометрическое распределение с математическим ожиданием и дисперсией .

Исходя из модели гипергеометрического распределения, в качестве статистики значимости мы используем асимптотически нормально (~N(0,1)) распределенную статистику Z=(N₁₁-E₁₁)/s. Для малых выборок эта статистика корректируется на основе прямого вычисления вероятностей так, чтобы для нее выполнялись соотношения нормального распределения.

Поскольку распределение этой Z-статистики асимптотически нормально, в дальнейшем мы будем работать с ним как с непрерывным распределением, допуская некоторую некорректность использовании этого, по природе дискретного, распределения.

Заметим, что при анализе таблиц, итоговые элементы которых сформированы не по объектам или, а также рассчитанных на основе взвешенных данных, мы будем в общем случае получать Z-статистики, не имеющие стандартного нормального распределения.

Z статистика отклонения средних

Рассматривая таблицы, построенные на основе неальтернативных признаков, мы изучаем каждую ячейку по отдельности, сравнивая среднее в группе, соответствующей ячейке, со средними в ее дополнении.

Обозначим A совокупность объектов, соответствующую i-тому ответу вертикального и j-му ответу горизонтального вопросов, B - ее дополнение. Число объектов в группе A равно . Группа объектов B может иметь разное содержание в зависимости от того, с чем мы хотим сравнить среднее в этой группе: 1) со средним по всей совокупности, тогда B - дополнение A до всей совокупности и содержит объектов; 2) с итоговым средним по строке, тогда B - дополнение A до i-той группы по вертикальному вопросу, а ; 3) с итоговым средним по столбцу, тогда B - дополнение A до j-той группы по горизонтальному вопросу, а .

Для проверки значимости различия средних в группах A и B в предположении теоретического нормального распределения, при несовпадении дисперсии в группах используется статистика 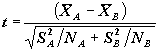, имеющая распределение Стьюдента с числом степеней свободы, зависящем от оценок дисперсии , и от объемов групп.

Статистика t характеризует отклонение среднего в группе A от среднего в группе B, но, поскольку , можно утверждать, что эта же статистика характеризует отклонение от итогового среднего . Вероятность среднего в ячейке быть меньше итогового среднего равна в условиях гипотезы независимости. Для получения нормально распределенной статистики Z мы используем формулу Z=Ф^-1(P{t<t_выб}), где Ф^-1 - обратная функция распределения нормального (N(0,1)) закона.

Здесь также как и при анализе частот имеет место замечание о некорректности утверждения о нормальности распределения Z-статистик в случае взвешенной выборки и вычисления итогов по ответам.

Уровень значимости связи и Z статистики

Таким образом, мы ввели измерители связи, имеющие одинаковое вероятностное распределение. На табл. 2 приведены значения Z статистик, которые могут в обычном анализе служить ориентирами для обнаружения связи в данных, в случае если ячейки изучаемых таблиц рассматриваются по отдельности.

Таблица 2. Критические точки для двустороннего Z - критерия

Связь	Очень слабая	Слабая	Наличие связи	Сильная связь	Очень сильная
P{|Z|>Zα }	0.1	0.05	0.01	0.005	0.001
Zα	1.64	1.96	2.57	2.81	3.29

По таблице 3, полученной на основе таблицы 1 легко видеть привязанность женатых к семье и меньшую ее ценность для всех остальных, а также серьезное отношение неженатых/незамужних к друзьям: соответствующие Z - статистики практически невероятно получить случайно.

Таблица 3. Z-статистики для смещений частот таблицы 1.

Жизненные ценности	Семейное положение
	Женат	Разведен	Вдовец	Холост
Друзья	-0,94	0,16	-2,29	3,17
Интересная работа	0,70	1,24	-2,18	-0,03
Семья	9,97	-5,27	-4,26	-6,16

В современном математическом обеспечении обычно не используют заранее заданного уровня значимости, а вычисляют наблюдаемый уровень значимости α_выб=P{|Z|>|Z_выб|}, вычисляемый по выборочным значениям Z. Величина 1-α_выб является значением F_|Z|(x) функции распределения |Z| в точке x=|Z_выб|, в свою очередь, F_|Z|(x)=2Ф(x)-1. Функция Ф(x) и ее модификации входят в стандартные наборы функций в языках программирования и в электронных таблицах.

В реальности приближенное равенство F_|Z|(x)=2Ф(x)-1 не всегда выполняется. При вычислении частот это возможно, например, при использовании «взвешенных» данных, а также при нарушении гипотезы нормальности при анализе смещений средних.

Множественные сравнения и перемешивание данных

Как следует из изложенного выше, рассматривая десять Z- статистик, с пороговым значение 1.96 (уровень значимости отдельной статистики равен 0.05), мы ошибочно можем обнаружить закономерность с вероятностью 0,4. По критерию Бонферрони, эту вероятность можно уменьшить до ~0.05, если использовать порог 2.81 (уровень значимости отдельной статистики равен 0.005).

В реальности зачастую независимости получаемых статистик нет. Если соответствующие переменные дублируют друг друга, то вероятность случайно обнаружить ложную закономерность при пороговом значении Z, равном 1.96 равна по-прежнему 0.05.

Так каким же порогом руководствоваться?

Сначала рассмотрим этот вопрос для анализа смещений частот.

В этом случае мы отталкиваемся от гипотезы отсутствия связи между дихотомическими переменными, соответствующие строкам, и переменными, соответствующими столбцам - гипотезы независимости строк и столбцов. Связь считается найденной, если получены значения Z-статистик, большие по абсолютной величине, чем даже маловероятные в условиях гипотезы максимальные по таблице значения |Z_ij|. При этом независимость переменных строк между собой и переменных столбцов между собой не предполагается.

Исследование связи происходит следующим образом:

1) назначается уровень значимости α_m;

2) исследуется вероятностное распределение величины 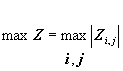, где Z_i,j значение Z-статистики в ячейке (i,j) таблицы;

3) оценивается квантиль maxZ=.

Максимум абсолютной величины Z-статистик из таблицы в условиях гипотезы может превзойти лишь с вероятностью α_m, поэтому это значение является критическим при оценке значимых связей.

Поскольку неясно, какова взаимосвязь между Z_i,j, теоретическое исследование распределения maxZ затруднено. Поэтому мы пользуемся статистическим компьютерным экспериментом.

Суть эксперимента состоит в многократном перемешивании данных, соответствующих одной из размерностей таблицы. Поясним, что означает перемешивание. Представим себе, что некоторая анкета состоит из двух (неальтернативных) вопросов, причем на одном листе – один вопрос, на другом – другой. После сбора данных листы первой части были рассыпаны, затем собраны и соединены со второй частью в произвольном порядке. Этот процесс имитируется на компьютере многократно.

В соответствии с этим экспериментом получается вариационный ряд {maxZ^(q)}, q=1…n_exp, где n_exp - число перемешиваний данных. Оценкой квантили порядка 1-α_m =m/n_exp, очевидно, может служить maxZ^(m). В случае, когда 1-α_m не является дробью, применяется линейная интерполяция квантили.

С точки зрения множественных сравнений оценка значимости средних ничем не отличается от оценки значимости смещений, однако, перемешивание данных осуществляется лишь по зависимой переменной.

Наблюдаемая множественная значимость

Как и в случае обычного исследования связи, наблюдаемым уровнем значимости является минимальное значение α_m, для которого наблюдаемое значение статистики остается значимым. Достаточно грубой оценкой наблюдаемой значимости выборочного значения Z_i,j,выб , в нашем случае, может быть α_m,выб=1-m/n_exp, гле m определяется номером ближайшего к |Z_i,j,выб| члена ряда {maxZ^(q)}, большего |Z_i,j,выб|_. Оценка α_m,выб может быть уточнена за счет линейного приближения α_m,выб с использованием maxZ^(q-1) и maxZ^(q).

К сожалению, если |Z_i,j,выб| больше максимума maxZ^(q), этот способ оценки α_m,выб не подходит, так как при этом неясно распределение таких "запредельных" значений maxZ.

Понижение требований к значимости, 1-й, 2-й … максимум.

Представим себе, что мы сравниваем k=400 независимых статистик (например, таблицу размерности 20x20). Ориентируясь на распределение максимальной статистики ½maxZ⁽⁴⁰⁰⁾½, при пороге значимости во множественных сравнениях a_m=0.05, нам придется признать незначимыми значения статистик, для которых a=1-(1-a_m)^1/k=0.00012823. Таким образом, при N(0,1) нормальном распределении Z критическим является значение ½Z½=3.83! Таким образом, ориентируясь на распределение максимума Z_ij, мы так сужаем число анализируемых статистик, что для анализа практически ничего не остается.

В действительности исследователь выбирает не одну статистику, а несколько. Подозрение должны вызывать ситуации, когда среди отобранных статистик значимых столько, сколько может быть в случайных данных. Исследователь может уменьшить критическое значение Z во множественных сравнениях, допустив среди отобранных по уровню значимости статистик некоторое небольшое число незначимых по отношению к критическому значению Z элементов. Формально это можно выразить следующим образом.

Упорядочим значения ½Z_ij½-статистик таблицы и получим ряд Z⁽¹⁾,…, Z^(k), в котором Z^(k)- максимальная из ½Z_ij½, а k совпадает с числом ячеек в таблице. В соответствии с введенными ранее обозначениями Z^(k)=maxZ. Для установления значимости на основании предложенной идеи мы будем рассматривать порядковые статистики Z^(k-1), Z^(k-2),… и т.д. Порядковую статистику Z^(k-s) будем называть s+1-м максимумом, а s+1-м критическим значением - величину , для которой . Таким образом, - значение, больше которого в условиях гипотезы независимости может оказаться более s значений Z_ij лишь с вероятностью .

В условиях независимости статистик Z_ij уровень значимости по s+1-му максимуму и обычный уровень значимости a находятся в следующем соотношении: . Поэтому здесь также может быть использован критерий, подобный критерию Бонферрони. Некоторую сложность представляет вычисление a по заданному значению , но это препятствие легко преодолимо с помощью компьютера. В качестве примера в табл.4 приведены критические значения для s=0,…,5 для 400 независимых Z-статистик.

Таблица 4. Критические оценки Z- статистик для множественных сравнений в обобщенном критерии Бонферрони

	k	s	a
0.05	400	0	0.00013	3.83
0.05	400	1	0.00089	3.32
0.05	400	2	0.00205	3.08
0.05	400	3	0.00342	2.93
0.05	400	4	0.00494	2.81
0.05	400	5	0.00655	2.72

Экспериментальная оценка критических значений проводится аналогично предыдущему. Для этого используется оценка распределения Z^(k-s), получаемого на основе перемешивания данных.

Бета - распределение для сглаживания и оценки наблюдаемой значимости в "недоступных" точках

Воспользуемся стандартным обозначением функции распределения F_x(x)=P{x<x} случайной величины x. Нетрудно показать, что для непрерывной случайной величины, в том числе для стандартной нормальной величины, Z распределение F_|Z| (|Z|) будет равномерным на отрезке (0,1). Значит распределение случайной величины U_ij=, связанной со значимостью Z-статистики ячейки таблицы, должно быть близко к равномерному на отрезке (0,1).

Случайная величина U^k-s= имеет распределение, являющегося "искажением" равномерного на отрезке (0,1) распределения: поскольку Z^k-s взято из правой части упорядоченного ряда {Z^q} статистик ½Z_ij½, плотность смещена к 1. Наши эксперименты с эмпирическими данными показали, что распределение U^k-s в условиях гипотезы независимости может быть описано бета-распределением, плотность которого имеет вид: B(x,a,b)=x^a-1(1-x)^b-1/B(a,b). Для независимых статистик ½Z_ij½, можно показать, что распределение U^k имеет плотность В(x,k,1), равномерное распределение U (U=U^k в ситуации, когда U_ij совпадают) является бета-распределением с параметрами a=1 и b=1.

Для оценки параметров распределения в общем случае используется результаты статистического эксперимента. С этой целью для сгенерированных значений статистик Z^k-s вычисляются U^k-s=. Полученная выборка позволяет оценить среднее и дисперсию U^k-s.

Известные формула для математического ожидания и дисперсии бета распределения [13] M=a/(a+b) и D=ab/((a+b)²(a+b+1)) позволяют выразить параметры a и b через математическое ожидание и дисперсию: a=(M²(1-M)-DM)/D и b=a(1-M)/M.

Подставляя в последнюю формулу оценки математического ожидания и дисперсии U^k-s, мы получаем оценки для параметров a и b.

Эксперименты, проведенные при перемешивании реальных данных, показывают, что в подавляющем большинстве случаев применение бета-распределения оправдано. Для иллюстрации этого мы воспользовались данными табл.1. Результаты применения 500-кратного перемешивания данных представляют собой выборку, в которой переменными являются с 1-го по 10-й максимум Z-статистик смещений частот. Значения этих переменных были заменены на соответствующие значения U^k-s. Мы проверили с помощью теста Колмогорова Смирнова соответствие распределения U^k-s бета-распределению. Таблица 5 показывает, что гипотеза о виде распределения не отклоняется. Конечно, в серии экспериментов возможно случайно получить значимые отличия – здесь тоже множественные сравнения! Но мы зачастую получали приемлемый результат: распределение сгенерированных значений U^k-s соответствовало теоретическому бета-распределению.

Таблица 5. Значимость критерия Колмогорова-Смирнова при проверке гипотезы о бета-распределении U^k-s (по результатам 500 экспериментов).

S	0	1	2	3	4	5	6	7	8	9
Наблюдаемая значимость	0.225	0.528	0.227	0.244	0.830	0.391	0.302	0.567	0.466	0.423

Благодаря полученной оценке параметров бета-распределения можно оценить наблюдаемую значимость и критические значения Z-статистик.

Оценка критического значения производится по следующему алгоритму

1. Оцениваются параметры a и b бета-распределения для U^k-s .

2. Решается уравнение , где функция бета-распределения, соответствующего U^k-s.

3. Решается относительно y уравнение F_|Z|(y)=x, это значение y будет искомым критическим значением .

Оценка множественной наблюдаемой значимости статистики ячейки Z_ij по s+1-му максимуму вычисляется по формуле .

Число степеней свободы

Как было указано выше, для независимых статистик множественная значимость связана с обычной значимостью формулой a_m=1-(1-a)^k»ka . Число независимых статистик k в этом случае можно вычислить из соотношения . Приближенно при небольших a_m можно положить k=a_m/a.. Если статистики значимости взаимосвязаны, то полученное таким образом значение f=a_m/a может трактоваться как скрытое в данных (в условиях гипотезы) число степеней свободы.

Хотя методику выбора номера статистики для анализа значимости еще необходимо определить на основании опыта, можно утверждать, что знание числа степеней свободы будет полезно для этой цели.

Примеры использования

Для иллюстрации метода были проведены множественные сравнения смещений частот и средних по данным, представленным в таблице 1.

Смещения частот. В результате 1000 экспериментов по перемешиванию данных выяснилось, что для 5% уровня значимости по 1-му максимуму критическим значением является =3,24 при 33 степенях свободы, в то время как таблица содержит 44 ячейки (табл. 6). Это конечно серьезное ограничение для отбора значимых статистик, однако выявленные закономерности весьма четки, поскольку вероятность посчитать значимым хотя бы одно отклонение частот в независимых данных равна 0.05. Второй и третий максимумы имеют, соответственно, критические значения 2.68 и 2.42. Таблица, полученная на независимых данных, будет с вероятностью 0.05 содержать 2,3… Z-статистики, больших по модулю 2.68 и 3,4… больших по модулю 2.42.

С содержательной точки зрения стоит обратить внимание на значимость связи семейного положения с приверженностью к семье, как к жизненной ценности. При обычном анализе (см. выше) отношение холостяков к друзьям рассматривалось бы как существенная закономерность безо всяких сомнений; в данном случае эта связь всплывает только при переходе к значимости по второму максимуму.

Таблица 6. Множественные значимости смещений частот таблицы “Что цените в жизни?” и “Ваше семейное положение?”

(Z-статистики, множественная значимость по 1-му максимуму (%)).

Жизненные ценности	Женат		Разведен		Вдов		Холост
	Z	a	Z	a	Z	a	Z	a
Друзья	-0,94	100,0	0,16	100,0	-2,29	60,5	3,17	6,4
Интересная работа.	0,70	100,0	1,24	100,0	-2,18	70,9	-0,03	100,0
Семья	9,97	0,0	-5,27	0,0	-4,26	0,1	-6,16	0,0
Материальное благополучие	1,76	96,6	0,86	100,0	-2,74	23,0	-0,93	100,0
Интересный досуг	-2,96	12,3	0,42	100,0	-0,89	100,0	4,14	0,2
Хорошие отношения	-2,06	81,1	1,61	99,1	1,36	100,0	0,50	100,0
Хорошее образование	-1,29	100,0	0,04	100,0	-0,56	100,0	2,24	65,3
Стабильность	1,18	100,0	-0,29	100,0	-1,50	99,7	-0,01	100,0
Свобода выбора	-0,31	100,0	0,17	100,0	-3,39	3,0	2,58	34,1
Здоровье	-2,16	72,7	0,17	100,0	2,84	17,5	0,32	100,0
Уважение окружающих	-1,98	86,8	2,01	84,8	2,01	84,8	-0,53	100,0

Следующий пример касается множественного сравнения средних. Для иллюстрации взяты группы, ранее представленные в таблице 1. В таблице 7 по этим группам представлены средний возраст, стандартная ошибка среднего и Z-статистики отклонений среднего от общего среднего. Здесь имеется возможность проанализировать статистики вместе с маргинальными оценками, полученными всей совокупности. Проведенные 1000 экспериментов показали, что критическим значением первого максимума является 3.44, второго – 2.93, третьего – 2.51. Вероятностная интерпретация полученных результатов аналогична интерпретации результатов, полученных для смещений частот. Характерно, что при множественном сравнении относительная молодость женатых любителей интересной работы не является неоспоримым фактом.

Таблица 7. Z-cтатистики отклонения среднего возраста в группах по семейному положению и ценностям (фрагмент данных).

Жизненные ценности	Женат	Разведен	Вдовец	Холост
Друзья	-4,32	-0,91	4,56	-9,65
Интересная работа	-2,43	0,57	6,73	-7,03
Семья	-4,41	-1,11	6,82	-8,23

Заключение

В данной работе мы намеренно сузили область применения разработанного метода, чтобы иметь возможность, во-первых, яснее обнажить проблему, во вторых, чтобы иметь возможность в реальное время подготовить программное обеспечение анализа множественных сравнений. В действительности решение проблемы следует распространить на исследование не только двумерных таблиц статистик, но и на многомерный случай, а также расширить множество анализируемых статистик.

К числу анализируемых параметров следует отнести параметры двухфакторного дисперсионного анализа, в котором факторами выступают дихотомические переменные. Нами рассмотрены лишь главные эффекты переменных и совместное их действие на зависимую переменную. В стадии решения находится проблема множественных сравнений эффектов взаимодействия факторов.

Использование статистического эксперимента не только открывает широкие анализа значимости, но и делает ранее некорректное использование статистических критериев корректным. В частности, это работа с взвешенными данными и таблицами со специфическими итоговыми элементами. Из-за этих особенностей вычисление Z-статистик становится формальной процедурой, тем не менее, их вычисление, как характеристик отклонения от ожидаемых значений оправдано. Благодаря вычислительному эксперименту происходит оценка распределения статистик и их значимости – недостаток теоретической базы восполняется за счет вычислительной мощи техники. Это же касается использования количественных переменных, не имеющих нормального распределения в сравниваемых группах объектов.

Литература

1. Чесноков С.В. Детерминационный анализ социально-экономических данных. -М.: Наука, 1988. -168 с.

2. SPSS Base 7.0 for Windows.Users Guide. Chicago, 1996. 939 p.

3. Ростовцев П.С., Костин В.С., Корнюхин Ю.Г., Смирнова Н.Ю. Анализ структур социологических данных и их устойчивости. В монографии «Социальная траектория реформируемой России. Исследования новосибирской эклномико-социологической школы. Новосибирск, Наука, 1999. с. 657-677.

4. Кендалл М.Дж., А.Стьюарт. Статистические выводы и связи. Глава 33. М. Наука, 1973. c.719-790.

5. Haberman Sh.J. Analysis of Qualitative Data. Vol. 1.New York: Academic press. 1978. p. 91-128.

6. Sobel M.E. Hand book of Statistical Modelling for the Social and Behavioral Sciencies. Chapter 5. The analysis of Contingency Tables. New York an London. Plenum Press. 1995. p.259-272

7. Миркин Б.Г. Анализ качественных признаков и структур. – М.: Статистика, с. 16-56.

8. Флейс Дж. Статистические методы для изучения таблиц долей и пропорций/ М.: Финансы и статистика, 1989.

9. Lerman I.C. (1980) Combinatorial Analysis in Statistical treatment of Behavioral Data. Quality and Quantity, vol. 14, No.3, p 431-469.

10. Ростовцев П.С. Статистическое согласование мер связи в анализе социально-экономической информации.// Экономика и математические методы. Том 26, М., 1991. 150-156.

11. Шеффе Г. Дисперсионный анализ. – М.: Наука, 1980. 512 с.

12. Lane T.P., DuMouchel W.H. Simultaneous confidence intervals in multiple regression: // The American Statistician, 1994 Vol.48, p.315- 321

13. Williams R.D. Multiple comparisons among correlation coefficients // The American Statistician, 1991. Vol.45, p.341- 341

14. SPSS for Windows. Chaid. Chicago, 1996. 148 p.

15. Ростовцев П.С., Костин В.С., Олех А.Л. Множественные сравнения в детерминационном и типологическом анализе. // Анализ и моделирование экономических процессов переходного периода в России. Выпуск 3.- Новосибирск, ИЭиОПП СО РАН, 1998. с.209-222.