П.С.Ростовцев, Костин
В.С., Корнюхин Ю.Г., Смирнова Н.Ю.
Анализ структур
социологических данных и их устойчивости
Исследование эмпирических
данных в социологии состоит в поиске взаимосвязей, оценке их существенность,
выявлении адекватных моделей распределений, построении группировок, выявлении
типологической структуры данных, иными словами идет поиск сведений,
представляющих структуру совокупности. В данной разделе мы рассмотрим методы и
алгоритмы, разработанные в отделе социальных пробен Института экономики и ОПП
СО РАН для анализа структур социально-экономических данных.
Основной упор в изложении
направлен на исследование устойчивости результатов анализа данных. Устойчивость
в данной работе рассматривается с точки зрения повторяемости результатов
исследования при повторном сборе данных, стабильности структур, найденных с
помощью работы алгоритмов.
Классические методы
проверки гипотез и вычисления интервальных оценок также связаны с проверкой
устойчивости. Проверка статистических гипотез дает возможность выяснить, не
может ли неустойчивость результатов исследования привести к фатальной ошибке -
коэффициент фиксирует связь, когда ее нет, понять, существенно ли структура,
модель распределения и ее элементы отличаются от предполагаемых. Подобные
аспекты устойчивости исследуются для весьма сложных моделей - факторного,
регрессионного, дисперсионного анализа и др. [1-4].
Классические методы
статистики развивались, когда вычислительная техника еще не имела достаточного
быстродействия, поэтому исследуемые статистики подбирались так, чтобы была
возможность оценить их распределения. В ряде случаев на генеральную
совокупность накладывались дополнительные ограничения (это касается
параметрических методов статистики [1-2]). Современные средства анализа
позволяют существенно расширить множество статистик и упростить расчеты. В
частности, для оценки значимости нередко нет необходимости проводить сложные
теоретические исследования распределений статистик, достаточно иметь мощный
компьютер и воспользоваться методом Монте-Карло либо провести прямые вычисления
вероятностей [5,6].
Данные социологических
исследований имеют особенности, затрудняющие применение традиционных методов.
Как бы хорошо не было спланировано исследование - распределение выборки обычно
оказывается смещенным по отношению к генеральной совокупности. Поэтому
приходится “ремонтировать” выборку, приводя пропорции в соответствие с
генеральной совокупностью. При таком “ремонте” из выборки выбрасывается часть
собранной информации или объектам приписываются веса, устраняющие диспропорции.
В первом случае часть средств затраченных на сбор данных выбрасываются “на
ветер”; во втором случае - мы лишаемся обычного математического аппарата
проверки статистических гипотез и исследования доверительных интервалов.
В настоящее время быстродействие
и память современного компьютера позволяют имитировать сложнейшие процессы,
моделировать случайные данные на компьютере (метод BootStrap) [7-9], работать
практически с любыми статистиками при минимальных ограничениях на распределение
генеральной совокупности, при этом смягчается проблема работы с “взвешенными”
данными.
Этот подход мы
демонстрируем на разработанных в ИЭиОПП СО РАН методах и программном
обеспечении, применяемом преимущественно для анализа социологических данных.
Для иллюстрации применения методов используются данные различных
социологических исследований, проведенных отделом социальных проблем Института
экономики и ОПП СО РАН.
Рассматриваемый подход в
наших работах нашел следующие применения.
1. Исследование
BootStrap-значимости элементов таблицы сопряженности и устойчивость ее
структуры. Таблицы сопряженности берутся в расширенном понимании - они
характеризуют связь между многозначными вопросами, в таблице может быть
размещен широкий круг статистик.
2. Изучение устойчивости
классификации, получаемой методом k-средних. Удается оценить устойчивость объектов, кластеров и кластерной структуры в
целом.
3. “Черно-белый” анализ
связи переменных. Для пары исследуемых переменных ищется дихотомическое
группирование, дающее наиболее контрастную таблицу сопряженности этих
дихотомий. Статистический эксперимент позволяет найти полутона в этом
“черно-белом” анализе.
4. Автоматизация
типологического группирования объектов. Входные данные программы включают
переменные для конструирования типологий и переменные для оценки качества
типологии. Здесь устойчивость используется как один из критериев оценки
качества группирования.
Целью раздела не является
полное решение определенных социологических задач, а изложение основных
элементов методов с демонстрацией их на простых примерах.
Основой для подготовки
данного текста послужили работы [10-13]
Данные
Обычно данные, рассматриваемые в
статистических пакетах - матрица 
(i=1,...,N;
j=1,...,m) по строкам которой расположены объекты (индекс i), а по столбцам -
переменные (индекс j), закодированные в виде числовых значений. Если часть
сведений о значениях переменных отсутствует, используются специальные коды
неопределенных значений.
В анкетных данных объекты соответствуют анкетам, а переменные, вообще говоря - вопросам. Особенностью анкетных данных является наличие многозначных (неальтернативных) вопросов, таких как вопрос “Что Вы цените в жизни?”. Ответы на эти вопросы кодируются не одним кодом, а несколькими, которые хранятся в нескольких обычных переменных.
Одна из переменных может играть роль весовой переменной.
Имитация сбора данных
Метод BootStrap [7] состоит в многократном повторении выборки данных из имеющихся данных и исследования поведения параметров совокупности. Если выборка хорошо представляет генеральную совокупность, то повторная выборка может пониматься как имитация повторного сбора данных. В каждом эксперименте генерируется выборка, объем которой совпадает с объемом исходных данных.
Так как производится выборка с возвращением, с извлечением новых объектов в исходной выборке данных не происходит изменения распределения. Генерированная же выборка будет иметь распределение, несколько отличающееся от распределения исходных данных. В ней будут те же исходные данные, но часть объектов повторится несколько раз, часть - не встретится ни разу. Из-за этого статистики, получаемые на данных, получат некоторое "возмущение".
Будем считать, что веса объектов при
генерировании выборки не меняются: если i-тый объект представлен в генерированной
выборке k копиями, то в этих копиях k раз повторилось
значение весового признака wi. Поэтому суммарный вес объектов в
экспериментах также может варьироваться случайным образом с математическим
ожиданием, равным 
, и дисперсией, равной 
. В невзвешенной выборке все объекты имеют единичный вес,
поэтому по условиям генерирования выборки суммарный вес всегда равен N.
Устойчивость статистик ячеек таблицы сопряженности
Элементы таблицы сопряженности.
Будем использовать запись
#A,
применяемую обычно для обозначения числа элементов множестве A,
для обозначения веса объектов в множестве объектов A.
Обычно таблица
сопряженности характеризует связь пары неколичественных переменных x
и y
[14] и содержит частоты (суммарные
веса) Ns,=#{x=s, y=t} объектов, имеющих одновременно
значения x=s и y=t. Мы расширили это определение
для описания связи неальтернативных
вопросов: Ns, в наших таблицах - это совместная частота (вес) ответов s и t на вопросы x
и y.
Для вычисления различных производных статистик используются также маргинальные
частоты (веса), которые для обычных альтернативных вопросов совпадают
соответственно с суммами по строкам и столбцам таблицы: 
и 
. Для неальтернативных
вопросов 
и 
- частоты (веса)
ответов s и t на вопросы x и y; для них приведенные
выше равенства, вообще говоря, не соблюдается.
Производные статистики -
это проценты, ожидаемые[1]
(в условиях независимости) частоты Est = Ns. N.,/N,
смещения Rst=Nst-Est и
др. Соотношение Rst>0 свидетельствует о наличии положительной
связи между s-м ответом вопроса x и t-м ответом вопроса y:
среди давших ответ s больше доля давших ответ t, чем в среднем по совокупности и
наоборот - среди давших ответ s больше доля давших ответ t,
чем в среднем по совокупности. Неравенство Rst<0
свидетельствует об обратной связи между
соответствующими значениями переменных (s-тым и t-м ответами).
Значимость смещений для
“невзвешенной” выборки можно оценить с помощью статистики Zst=(Nst-Est)/s, где дисперсия вычислена исходя из
гипергеометрического теоретического распределения Nst. Для
больших выборок Zst имеет приближенно стандартное нормальное
распределение; для малых выборок значения Zst нами корректируются
на основе прямого вычисления вероятностей. Если не учитывать множественных
сравнений, то для непосредственной оценки значимости отдельных выборочных
значений 
можно использовать
вероятности pst=
. Значение pst, близкое к нулю свидетельствует об
существенно малом выборочном значении Nst по сравнению с ожидаемым значением Est
: маловероятно случайно (в условиях независимости) получить это
значение меньше выборочного. Значение pst, близкое к единице - свидетельство
относительно большого значения Nst по сравнению с ожидаемым: почти всегда
случайно получаемые значения Nst меньше выборочных.
В таблицах мы можем также
размещать описательные статистики количественных переменных (средние 
, стандартные отклонения и др.), а также z-статистики отклонений
среднего в ячейке от среднего по всей совокупности объектов 
или от средних по
строкам или столбцам таблицы (
или 
) и оценки наблюдаемой значимости этих отклонений pst.
Для вычисления значимости смещений среднего в группе объектов мы находим
наблюдаемую значимость разности средних в этой группе и ее дополнении
(используется распределение Стьюдента, а поэтому предполагается нормальность
распределения суммируемой переменной).
В терминах дисперсионного
анализа можно интерпретировать
вероятности pst в зависмости от поставленной задачи как
значимости эффектов совместного действия значений переменных или эффектов
действия значений одной переменной (ответа на один вопрос) при условии значения
другой переменной (ответа на другой вопрос).
Как уже было отмечено,
традиционные методы вычисления вероятностей, в данном случае, корректны лишь
для невзвешенных данных, кроме того использование параметрических методов
предполагает нормальность распределения генеральной совокупности, что является
также жестким ограничением.
Вычисление
BootStrap-значимости
Будем помечая звездочкой статистики,
полученные на генерированной выборке: накопленные частоты (веса) в ячейке (s,t) таблицы сопряженности на
генерированных данных - 
; 
и 
- маргинальные
частоты (веса); N* - суммарный вес генерированных объектов; 
=
/N* -”ожидаемые” веса 
и 
=
-
- смещения “наблюдаемых” частот.
Если в большой доле экспериментов 
имеет один и тот же
знак, естественно считать, что обнаружена устойчивая связь.
Если в ячейках таблицы находятся средние 
некоторой суммируемой
переменной u, и имеются маргинальные значения 
, 
и 
, то определим смещение среднего 
как 
-
, 
-
или 
-
от общего среднего, от среднего по строке и среднего по
столбцу. Здесь постоянство знака 
свидетельствует об
устойчивом влиянии факторов на суммируемую переменную.
Валидность эксперимента. В ряде
случаев результаты эксперимента могут оказаться неприемлемыми для вычисления
статистики 
. При вычислении смещений частот это происходит, если
маргинальные частоты оказываются равными нулю: 
=0 или 
=0. В этом случае нет шансов получить ненулевого смещения 
. При вычислении смещений средних неприемлем случай, когда 
=0. В этих случаях невозможно вычислить средние.
Эксперименты, в которых имеет смысл
вычислять статистику 
, будем называть валидными экспериментами. Число
валидных экспериментов определяется для каждой ячейки таблицы.
BootStrap-значимость. Пусть
произведено Mэ валидных экспериментов по случайному
генерированию данных, в которых Kэ раз оказывалось, что 
>0 (Kэ=#{
>0}).
Назовем BootStrap-значимостью
смещения и обозначим ab долю экспериментов, в которых 
>0 : ab= Kэ/Mэ .
Пример: значимость и
BootStrap-значимость
Табл.1 содержит основные
статистики для оценки взаимосвязи по таблице сопряженности неальтернативных
вопросов (данные “невзвешены”). Обратим внимание, к примеру, на клетку
таблицы “друзья”-“вдовые”. В условиях
независимости ожидаемая частота равна 40.83,
в то время, как наблюдаемая - 28.
Смещение - 12.83, наблюдаемая значимость смещения по критерию Фишера
равна 0.003, Bootstrap - значимость (100 экспериментов) - 0.00. Таким образом,
в соответствии с точным критерием Фишера, большее отрицательное смещение, чем
наблюдаемое в условиях независимости можно получить лишь с вероятностью 0.003,
в экспериментах по имитации сбора данных ни разу не получена связь обратной
направленности.
Таблица 1. Фрагмент таблицы сопряженности вопросов “Что цените в жизни?” и “Ваше
семейное положение?”. Частоты, проценты по горизонтали и по вертикали,
значимость, Bootstrap - значимость (100 экспериментов)
|
Жизненная
ценность |
женат |
разведен
|
вдовец |
холост |
Всего |
|
друзья |
|
|
|
|
|
|
Частота |
377 |
40 |
28 |
69 |
515 |
|
%по строке |
73.2% |
7.8% |
5.4% |
13.4% |
42.5% |
|
%по столбцу |
41.9% |
44.0% |
29.2% |
56.1% |
|
|
значимость |
0.240 |
0.613 |
0.003 |
0.999 |
|
|
bootstr.-знач. |
0.160 |
0.580 |
0.000 |
1.000 |
|
|
интересная
работа |
|
|
|
|
|
|
Частота |
345 |
40 |
24 |
47 |
456 |
|
%по строке |
75.7% |
8.8% |
5.3% |
10.3% |
37.7% |
|
%по столбцу |
38.4% |
44.0% |
25.0% |
38.2% |
|
|
значимость |
0.810 |
0.901 |
0.004 |
0.553 |
|
|
bootstr.-знач. |
0.830 |
0.920 |
0.000 |
0.660 |
|
|
семью |
|
|
|
|
|
|
Частота |
721 |
45 |
49 |
61 |
878 |
|
%по строке |
82.1% |
5.1% |
5.6% |
6.9% |
72.5% |
|
%по столбцу |
80.2% |
49.5% |
51.0% |
49.6% |
|
|
значимость |
1.000 |
0.000 |
0.000 |
0.000 |
|
|
bootstr.-знач. |
1.000 |
0.000 |
0.000 |
0.000 |
|
|
мат.
благосостояние |
|
|
|
|
|
|
Частота |
376 |
42 |
24 |
46 |
489 |
|
%по строке |
76.9% |
8.6% |
4.9% |
9.4% |
40.4% |
|
%по столбцу |
41.8% |
46.2% |
25.0% |
37.4% |
|
|
значимость |
0.959 |
0.878 |
0.001 |
0.239 |
|
|
bootstr.-знач. |
0.960 |
0.810 |
0.000 |
0.270 |
|
|
здоровье |
|
|
|
|
|
|
Частота |
469 |
51 |
62 |
68 |
652 |
|
%по строке |
71.9% |
7.8% |
9.5% |
10.4% |
53.8% |
|
%по столбцу |
52.2% |
56.0% |
64.6% |
55.3% |
|
|
значимость |
0.024 |
0.669 |
0.986 |
0.633 |
|
|
bootstr.-знач. |
0.000 |
0.670 |
0.990 |
0.670 |
|
|
Всего |
|
|
|
|
|
|
Частота |
899 |
91 |
96 |
123 |
1211 |
|
%по строке |
74.2% |
7.5% |
7.9% |
10.2% |
100.0% |
Еще пример - отношение
вдовых к здоровью. Из табл.1, видим, что среди вдовых 64.6% считают жизненной
ценностью здоровье, в то время, как в целом по совокупности - 53.8%. Значимость
смещения - 0.986, Bootstrap - значимость равна 0.99. Это
свидетельствует о том, что вдовые (скорее всего люди пожилые) больше пекутся о
здоровье, чем все остальное население.
Легко видеть, что
Bootstrap-значимость мало отличается от значимости по точному критерию Фишера,
причем это можно отметить практически для всей таблицы. Близость оценок
свидетельствует о правомерности применения метода Bootstrap.
Обычно социологи для
описания своих результатов пользуются процентным распределением, однако нередко
неясно, существенно ли смещение процентов. Вычисляемая нами значимость позволяет
нам уберечься от ошибок, когда кажущееся большим смещение переменных в
действительности несущественно.
Таблица 2. Средний возраст в группах по ответам на вопросы “Что цените в жизни?” и
“Ваше семейное положение?”, значимости отклонения среднего по отношению к
средним в группах по семейному положению, Bootstrap-значимость (100 эксп.)
|
|
женат |
разве-ден |
вдовец (вдова) |
холост (не за-мужем) |
по всей совокупности |
|
друзей |
40.22 |
41.28 |
55.82 |
26.00 |
39.24 |
|
значимость |
0.000 |
0.079 |
0.001 |
0.001 |
|
|
bootstr.-знач. |
0.000 |
0.120 |
0.000 |
0.000 |
|
|
работу |
41.27 |
43.62 |
61.58 |
28.38 |
41.21 |
|
значимость |
0.016 |
0.674 |
0.324 |
0.238 |
|
|
bootstr.-знач. |
0.000 |
0.660 |
0.400 |
0.190 |
|
|
семью |
41.13 |
41.27 |
58.45 |
27.41 |
41.16 |
|
значимость |
0.000 |
0.057 |
0.000 |
0.046 |
|
|
bootstr.-знач. |
0.000 |
0.080 |
0.000 |
0.030 |
|
|
матер.благополуч |
40.53 |
41.60 |
58.50 |
29.76 |
40.50 |
|
значимость |
0.000 |
0.109 |
0.056 |
0.599 |
|
|
bootstr.-знач. |
0.000 |
0.110 |
0.030 |
0.570 |
|
|
здоровье |
43.47 |
44.08 |
63.10 |
30.60 |
44.06 |
|
значимость |
0.991 |
0.852 |
0.792 |
0.889 |
|
|
bootstr.-знач. |
0.980 |
0.840 |
0.770 |
0.960 |
|
|
По
всей совокупности |
42.45 |
43.06 |
62.35 |
29.38 |
42.76 |
Табл.2 содержит данные по
среднему возрасту респондентов в группах по ответам на вопросы “Что Вы цените в
жизни?” и “Ваше семейное положение?”. Значимость и Bootstrap-значимость
отклонения вычислялись внутри групп по семейному положению.
В частности, средний возраст холостяков - 29.38, однако те из них, кто считает ценностью семью, имеют средний возраст - 27.41, значимость - 0.046 (вероятность при определенных предположениях случайно получить большее отрицательное смещение), и Bootstrap-значимость - 0.03 (доля экспериментов, в которых средний возраст холостяков (незамужних), ценящих семью, превысил средний возраст не состоящих в браке.
Несмотря на не вполне корректные предположения о нормальности параметрические оценки значимости и результаты статистических экспериментов оказались весьма близки.
Устойчивость кластерной структуры
Кластерный
анализ является одним из методов математической обработки данных, полезный для
типологического анализа совокупности. Обнаруженные этим методом "сгустки
объектов", называемые кластерами (классами, таксонами), позволяют
сформулировать, в конечном счете, гипотезы о логической структуре совокупности.
Точным обоснованным
выводам о кластерной структуре уделяли внимание Бокк и Хартиган [16, 18] - их
исследования показывают сложность решения проблемы традиционными
параметрическими методами. В данном разделе мы уделим внимание исследованию
устойчивости результатов работы распространенного метода - метода "k
средних" [15].
Алгоритм кластеризации
Алгоритм позволяет
изучать большие массивы данных, не ограничивающиеся возможностями оперативной
памяти ЭВМ. Его целью является - минимизация разброса внутри кластеров.
Локальную оптимизацию этого критерия осуществаляет алгоритм k-средних.
Наш вариант этого алгоритма состоит в следующем:
1) выбираются k объектов - центров
кластеров;
2) каждый объект
относится к кластеру, расстояние до центра которого минимально;
3) вычисляются новые
центры кластеров - средние арифметические по их объектам;
4) если хотя бы один
объект переместился в другой кластер - осуществляется переход к п.1), в
противном случае алгоритм заканчивает свою работу.
Начальные центры
выбираются следующим образом:
вычисляется центр тяжести совокупности объектов; в качестве первого
центра берется наиболее удаленный центра тяжести объект; в качестве i-того
центра берется объект, минимальное расстояние которого от 1, 2, ...,i-1-го центров
- максимально.
Для вычисления расстояний
используется эвклидово расстояние. При наличии пробелов в данных при вычислении
расстояний используются только те переменные, значения которых определены;
расстояния нормируются в соотвествии с числом определенных переменных. Если
данные “взвешены”, то при вычислении центров тяжести учитываются веса объектов.
Исходная и "возмущенная”
кластерные структуры
Допустим, мы провели
кластерный анализ совокупности, получив исходную кластерную структуру. Это
означает, что мы каждому объекту Xi приписали номер
кластера r(i).
Поскольку объекты
генерированной совокупности (выборки с возвращением) являются объектами
исходной совокупности, то и генерированная совокупность расклассифицирована в
соответствии с номерами r(i). Эта классификация не будет
оптимальной.
Используя в качестве
начального разбиения на генерированной совокупности эту классификацию, можно
применить алгоритм кластерного анализа. Здесь кластерам исходной классификации R={R1,...,Rk}
соответствуют кластеры генерированной классификации S={S1,...,Sk}
с центрами, вообще говоря, не совпадающими с исходными.
По тому, насколько
изменится исходная кластерная структура, насколько не совпадают R
и S,
можно судить о ее устойчивости. Однако, как замечено выше, часть объектов
исходных данных в генерированных данных отсутствует.
Полную информацию о
кластерной структуре содержат центры кластеров. Поэтому обратный переход
происходит следующим образом. В качестве центров кластеров “возмущенной”
кластерной структуры берутся центры классов S1,...,Sk; объекты
исходной совокупности распределяются в соответствии с методом k
средних (шаг 2) по близости к центрам. В соответствии с этой классификацией
каждый объект исходной совокупности Xi получит номер кластера
s(i).
Статистики устойчивости.
Пусть проведено M
экспериментов. Рассмотрим частоты m1(i),...,mk(i),
с которыми объект Xi оказывался в классах S1,...,Sk соответственно.
Величину Pr(i,l)=ml(i)/M
назовем степенью предпочтения i-тым объектом l-го класса. Эта величина
является, при сделанных предположениях о репрезентативности выборки, оценкой
вероятности смены объектом Xi кластера при l,
не совпадающим с r(i), и вероятностью остаться в кластере при значении l,
равном r(i). Стабильность объекта, таким образом, характеризуется
степенью предпочтения i-м объектом класса r(i)
(класса исходной классификации) - Pr(i,r(i)).
Вероятно, с точки зрения
социологии, предпочтения Pr(i,l) отражают возможность
нечеткого отнесения объекта к тому или иному типу объектов, пограничное состояние
в той или иной социальной группе.
Стабильность кластеров.
Обозначим Mlt
- суммарный вес объектов (с учетом повторов), перешедших из Rl
в St
во всех экспериментах. В случае невзвешенной выборки - это число переходов
объектов из Rl в St.
Доля переходов из класса Rl
в класс St - Prt(St/Rl)=Mlt/Ml.
- является оценкой вероятности соответствующего перехода, здесь Ml.
- сумма элементов ||Mlt|| по строке (вес исходов из Rl).
Стабильность класса Rl
характеризует величина Prt(Sl/Rl).
Стабильность/нестабильность классификации.
Стабильность Stb(R)
классификации в целом мы оцениваем долей веса объектов, оставшихся в исходных
кластерах: Stb(R) =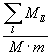 
,где m
- общий вес всех объектов.
Нестабильность, или
оценка вероятности объектов не перейти в другой класс, оценивается по формуле: Ust(R)=1-Stb(R)
В настоящее время еще не
накоплен опыт в определении, какой уровень стабильности/нестабильности
удовлетворителен, какой - неудовлетворителен. Традиции в данной области
сложатся в результате опыта обработки конкретных данных, а также исходя из
экспериментов по кластерному анализу специального вида данных, которые могут
быть представлять стандарт (однородные равномерные данные, многомерная
нормальая совокупность).
Доверительные интервалы - вторичные
статистики.
Характеристики
устойчивости объектов Pr(i,l), классов Prt(St/Rl)
и классификации в целом Stb(R) можно рассматривать с точки
зрения наличия генеральной совокупности - результата бесконечного числа
экспериментов, считая эти показатели оценками соответствующих параметров,
полученных на выборке объема M. При этом подходе целесообразно
вычислить доверительные интервалы "истинных" значений параметров и
стандартные ошибки их оценок.
В частности,
доверительные интервалы вероятности p(i,l) объекта Xi случайно
перейти в класс Sl получаются на основании статистики fl(i),
имеющей биномиальное распределение с параметрами M и p(i,l) - Bin(M,p(i,l)).
Оценкой p(i,l) является Pr(i,l), а ее стандартной ошибкой - SQRT(Pr(i,l)(1-Pr(i,l)/M).
Математическое ожидание EStb(Rl,St)
доли объектов класса Rl, перемещающихся в
класс St оценивается средним значением - долей в каждом
испытании - Stb(Rl,St). Для оценки доверительных
границ EStb(Rl,St) следует воспользоваться
приближенной нормальностью долей в каждом испытании (при большом объеме
исходной совокупности) и распределением Стьюдента (попутно будет вычислена и
стандартная ошибка оценки).
Аналогичным образом можно поступить,
оценивая "истинное" значение нестабильности классификации в целом.
Пример использования метода в анализе анкетных данных
Для анализа взяты
дихотомические переменные, соответствующие ответам на вопрос “Что Вы цените в
жизни?” (из заданного списка выбиралось не более 4-х подсказок). Результат
кластерного анализа представлен табл.3, содержащей центры полученных кластеров.
Таблица 3. Центры
классификации методом k средних
|
Название |
Центры классов |
Центр |
||
|
переменной |
Класс 1 |
Класс 2 |
Класс 3 |
совокупности |
|
свобода |
0.615 |
0.099 |
0.353 |
0.243 |
|
будущее детей |
0.410 |
0.888 |
0.173 |
0.631 |
|
карьера |
0.333 |
0.007 |
0.045 |
0.066 |
|
семья |
0.436 |
0.747 |
0.128 |
0.540 |
|
мат.благосост. |
0.974 |
0.428 |
0.180 |
0.447 |
|
власть |
0.026 |
0.000 |
0.015 |
0.008 |
|
здоровье |
0.205 |
0.724 |
0.707 |
0.641 |
|
любимое дело |
0.154 |
0.184 |
0.466 |
0.252 |
|
Всего объектов |
78 |
304 |
133 |
515 |
Так как переменные
принимают только значения 0 и 1, значения средних соответствуют доле респондентов,
принимающих ту или иную ценность, в частности доля респондентов, ценящих
свободу в классе 1 равна 0.615.
Табл.3 позволяет придать
следующую интерпретацию кластерам. Кластер 1 характеризует тип респондентов
ценящих более остальных свободу, карьеру, материальное благосостояние, власть;
кластер 2 - респонденты предпочитающие семейные ценности - детей, семью,
здоровье; кластер 3 выделяется ценителями любимого дела, высока доля тех, кто
считает ценностью здоровье, и высока доля любителей свободы.
В результате проведения
100 экспериментов выяснилось, что устойчивость полученной классификации равна
95.08%. Велика ли эта устойчивость? Для сравнения скажем, что выборка из
8-мерного нормального распределения с единичной ковариационной матрицей дала в
тех же условиях устойчивость 86.6%. Опыт экспериментов с искусственными данными
однокластерной структуры показал, что разброс результатов здесь невелик
(1.5-2%) и наши результаты можно считать устойчивыми.
Табл.4 показывает
устойчивость каждого кластера (по диагонали), а также, насколько объекты
каждого кластера тяготеют к другим кластерам.
Таблица
4.
Перемещения объектов между кластерами (в процентах к общему
числу)
|
Перемещения в |
Перемещения из кластера |
||
|
кластер |
1 |
2 |
3 |
|
1 |
97.18 |
0.75 |
1.03 |
|
2 |
0.99 |
93.89 |
2.38 |
|
3 |
1.83 |
5.36 |
96.59 |
|
Всего |
100.00 |
100.00 |
100.00 |
Полезно рассмотреть
конкретные неустойчивые объекты и попытаться понять причины их неустойчивости.
В табл.5 приведен, пример нескольких неустойчивых объектов кластера 2, коды
значений переменных указаны в соответствии с порядком табл.3. Напомним, что
второй кластер характеризуется семейными ценностями: дети, семья, здоровье.
У первого объекта “не
отмечена” единичкой такая ценность, как будущее детей, но “отмечены”
материальное благосостояние и любимое дело. Вероятно поэтому он 51 раз из 100
оказывался в кластере 3 и один раз - в кластере 1. Он внес большой вклад в
неустойчивость классификации, поскольку в данных он встречается 10 раз, а его
устойчивость всего 0.48.
Второй объект -
характерен тем, что здесь “отмечена” единственная ценность - семья. Это,
по-видимому, также послужило причиной его малой устойчивости (0.51).
Третий объект явно
тяготеет к первому кластеру (с частотой 36), так как здесь присутствуют такие
ценности, как карьера и материальное благополучие.
Таблица 5. Примеры неустойчивых объектов
|
Значения |
|
Перемещений в кластер |
|
|
||
|
переменных |
Кластер |
1 |
2 |
3 |
Устойчивость |
Частота |
|
0 0 0 1 1 0 1 1 |
2 |
1 |
48 |
51 |
0.48 |
10 |
|
0 0 0 1 0 0 0 0 |
2 |
1 |
51 |
48 |
0.51 |
8 |
|
0 1 1 0 1 0 1 0 |
2 |
36 |
64 |
0 |
0.64 |
1 |
Кластерная карта матрицы данных и ее использование в анализе таблиц сопряженности
Матрицы данных небольшого
объема нередко не требуют специальных средств автоматизации анализа, однако
таблица размерности 20х20 уже пестрит цифрами и требуется искусство и опыт для
обобщения и упорядочения материала. В данной разделе мы рассмотрим метод и
программное средство упорядочения данных и специального вида кластерного
анализа. Преимуществом предлагаемого подхода к решению данной задачи по
отношению к имеющимся разработкам [16,17] в наименьших ограничениях на форму
кластера.
Упорядочение строк и столбцов,
однородные области
Предполагается, что
элементы матрицы данных сравнимы между собой. Анализ матрицы проводится в два
этапа.
Первый этап состоит в упорядочении строк и столбцов для придания таблице данных “непрерывного” вида.
Обозначим 
- анализируемую
матрицу; 
- эвклидово
расстояние между строками; 
- эвклидово
расстояние между столбцами.
Естественно считать хорошо
структурированной таблицу, в которой не очень часто происходят скачки между
значениями соседних элементов, поэтому для лучшей структурированности таблицы
целесообразно переставить строки и столбцы матриц так, чтобы расстояние между
соседними строками 
и расстояние между
соседними столбцами 
в сумме было
небольшим.
На основании этих соображений наш
критерий качества упорядочения строк - это сумма расстояний между строками 
. Поэтому цель первого этапа анализа матрицы состоит в поиске
такой перестановки (i1,..im) строк, чтобы 
. Для поиска такой перестановки в реальное время нами
используются локально-оптимальные алгоритмы, применяемые в теории графов при
решении задачи “коммивояжера” [19]. Аналогичная операция проводится со
столбцами.
Второй этап состоит в объединении
элементов матрицы в связные области (кластеры). Пусть 
- разбиение таблицы
на связные области; 
- средняя величина элементов области 
. Критерием качества разбиения в нашей работе является
величина остаточного разброса при аппроксимации таблицы средними значениями
элементов областей 
. Для построения используется агломеративный алгоритм, после
применения которого дополнительно передвигаются границы кластеров.
Пример: структура Z-смещений
В качестве примера приведем структуру матрицы Z-смещений (табл.6), в которой упорядочены столбцы и строки и получена ее кластерная карта. Двойной линией обведены области; номера областей расположены на линиях, ограничивающих области сверху.
Область 0 обращает внимание на существенную положительную связь между ценностью “семья” и значением “женат” переменной “семейное положение”, а область 1 - на отрицательную связь ценности “семья” со значениями “разведен”, “вдовец” и “холост”, которые можно объединить одним термином - “несемейные”. Другими словами, выделение этих двух областей подчеркивает факт ценности семьи для семейных и неценности для несемейных.
Область 3 демонстрирует низкую привлекательность работы для вдовых (до работы ли старикам?). Область 5 свидетельствует о том, что у семейных ценности досуга заменены другими, зато область 4 показывает, что холостяки ценят и досуг и свободу выбора (но последнее не очень значимо), а разведенные - работу и несколько меньше досуг. Области 7 и 8 обращают наше внимание на то, что вдовые ценят уважение и отношения между людьми, а женатые относятся к этому более прохладно.
Таким образом, в данном случае разделение на области акцентировало внимание на определенных закономерностях.
Таблица 6. Структура однородных областей таблицы Z-отклонений
┌────────────────┬────────┬────────┬────────┬────────┐
│ │женат │вдовец │разведен│холост
│
│ │ │ │
│ │
├────────────────┼────────┼────────┼────────┼────────┤
│
╔(0)═════╦(1)══════(1)══════(1)═════╗
│семья ║ 6.4 ║ -2.8
-2.8 -3.8 ║
│
╠(2)═════╩(2)══════(2)══════(2)═════╣
│стабильность ║
1.5 -1.4 0.4
-1.7 ║
│ ║
╔(3)═════╦(4)═════╗ ║
│работа ║ -0.6 ║
-3.5 ║ 2.9
║ 0.2 ║
│
╠(5)═════╬(6)═════╣
╚(4)═════╣
│досуг ║ -3.4 ║ -1.3
║ 1.7 3.7
║
│
╠(6)═════╝
╚(6)═════╗ ║
│свободу
выбора ║ -0.2
-1.5 -0.2 ║ 1.4 ║
│ ║
╚(6)═════╣
│матер.благополуч║ 0.7
-0.8 -0.3 -0.1
║
│ ║ ║
│здоровье ║ 1.2 -0.1 -1.6
-0.1 ║
│ ║ ║
│образование ║
-0.7 -0.1 0.2
0.9 ║
│ ║ ║
│друзья ║ -0.7 0.6 -0.2
0.7 ║
│
╠(7)═════╦(8)═════╗ ║
│уважение ║ -2.9 ║ 3.2
║ 1.1 0.6
║
│ ║ ║ ╚(8)═════╗ ║
│отнош.между
людь║ -2.0 ║
3.1 1.6 ║
-1.1 ║
│ми
╚════════╩═════════════════╩════════╝
└────────────────┴────────┴────────┴────────┴────────┘
Из-за грубости представления информации (числа областей), "упущений", связанных с локальной оптимальностью алгоритма, может быть допущена некоторая неоднородность областей, (например, положительное отношение женатых и отрицательное отношение холостых к стабильности, обл.2).
Устойчивость областей
Элементы таблицы сопряженности на генерированных данных испытывают некоторое “возмущение”, испытывает “возмущение” и кластерная структура.
Начнем с описания проверки устойчивости областей при условии, что сохраняется порядок строк и столбцов, полученный при упорядочении исходной таблицы.
Эксперимент по проверке устойчивости областей состоит в следующем. Генерируются данные, по ним получается таблица статистик. На этой таблице задается структура областей, полученная на исходных данных. Эта структура улучшается за счет перемещения границ областей, в ходе которой минимизируется остаточная дисперсия.
Пример: устойчивость структуры Z-смещений
Изменения структуры областей характеризует устойчивость результата. Рис.1 иллюстрирует указанные эксперименты при исследовании структуры связи значений признака "жизненные ценности" и "семейное положение". Схемы областей в экспериментах изменяются, но основная часть элементов не перемещалась в другие области.
Рис
1. Эксперименты по проверке
устойчивости структуры областей таблицы
Z-отклонений (связь жизненных
ценностей и семейного положения, табл.3).
╔0╦1════╗
╔0╦1════╗
╔0╦1════╗
╔0╦1════╗ ╔0╦2══╦1╗
╔0╦1════╗
╠2╩═════╣
╠2╩═════╣
╠2╩═════╣
╠2╩═════╣ ║ ║
╔4╣ ║ ╠2╩═════╣
║ ╔3╦4╗
║ ║
╔3╦4╗ ║ ║ ╔3╦4╗ ║
╠3══╦4╗ ║ ╠3╩═╣
╚═╣ ║ ╔3╦4╗ ║
╠5╬6╣
╚═╣
╠5╬6║ ╚═╣
╠5╩═╣ ╚═╣ ╠5╗ ║
╚═╣ ╠5╦6╣
║ ╠5╣ ║ ╚═╣
╠═╝
╚═╗ ║
╠═╝ ╚═══╣
╠6╗ ╠═══╣ ╠6╣
╠═╗ ║ ╠═╝ ╚═╗
║ ╠6╣ ╠═══╣
║ ╚═╣
║ ║ ║
╚═╝ ║ ║
║ ║ ╚═╣ ║ ╚═╣ ║ ║ ║ ║
║ ║
║ ║
║ ║ ║
╚═╝ ║
║ ║ ║
╚═╝ ║
║ ║
║ ║
║ ║ ║ ║ ║
╔8══╗ ║ ║ ║
║ ║ ║
╔8╗ ║ ║ ║ ║ ╔8╗ ║ ║ ║
╔═╝ ║ ║
║
╠7╦8╗ ║
╠7╣ ╚═╗ ║
╠7╦8╗ ║
╠7╣ ╚═╗ ║ ╠7╣
╚═╗ ║ ╠7╦8══╗ ║
║ ║ ╚═╗
║ ║ ║ ║ ║ ║ ║
║ ║ ║ ║ ║ ║ ║ ║
╔═╝ ║ ║ ║ ╔═╝ ║
╚═╩═══╩═╝
╚═╩═══╩═╝
╚═╩═╩═══╝ ╚═╩═══╩═╝
╚═╩═╩═══╝
╚═╩═╩═══╝
Исходная 1 2 3 4 5
структура структуры в пяти экспериментах
Таблица 7. Частоты перемещений из областей
элементов таблицы
┌────────────────┬────────┬────────┬────────┬────────┐
│ │женат
│вдовец
│разведен│холост
│
├────────────────┼────────┼────────┼────────┼────────┤
│
╔(0)═════╦(1)══════(1)══════(1)═════╗
│семью ║
0 ║ 23
6 0 ║
│
╠(2)═════╩(2)══════(2)══════(2)═════╣
│стабильность ║ 7 5 6 12 ║
│ ║
╔(3)═════╦(4)═════╗ ║
│работу ║ 34 ║
3 ║ 2 ║
22 ║
│
╠(5)═════╬(6)═════╣
╚(4)═════╣
│досуг ║
3 ║ 65
║ 9 4
║
│
╠(6)═════╝
╚(6)═════╗ ║
│свободу выбора ║
19 65 9
║ 22 ║
│ ║
╚(6)═════╣
│матер.благополуч║ 1
33 15 4
║
│ ║ ║
│здоровье ║ 0 12 18 0 ║
│ ║ ║
│образование ║ 11 11 10 0 ║
│ ║ ║
│друзей ║ 35 29 3 0 ║
│
╠(7)═════╦(8)═════╗ ║
│уважение ║ 3 ║ 2
║ 45 0
║
│ ║
║
╚(8)═════╗ ║
│отнош.между людь║ 2
║ 1 39
║ 0 ║
│
╚════════╩═════════════════╩════════╝
└────────────────┴────────┴────────┴────────┴────────┘
Обобщает результаты
экспериментов табл.7 частот перемещения
элементов из областей (табл.3) в другие области.
В качестве примера
интерпретации заметим, что кластер 7 - относительно устойчив - ячейки “уважение
- женат” и “отношение между людьми - женат” уходили из кластера только 3 и,
соответственно 2 раза; в кластере 8 неустойчива ячейка “отношение между людьми
- разведен” (36 перемещений), ячейки “уважение - вдов” и “отношение между
людьми - вдов”.
Устойчивость порядка строк и столбцов.
Для оценки устойчивости строки и столбцы таблицы на генерированных данных упорядочиваются в соответствии с ранее полученным упорядочением исходной таблицы.
Далее поочередно рассматривается каждый столбец. Для столбца вычисляется, в какое место таблицы, за каким столбцом, его целесообразнее всего поместить. При повторении экспериментов накапливаются частоты, с которыми i-й столбец было “целесообразно” переместить на j-е место.
Аналогичная процедура проделывается со строками.
Пример. Устойчивость порядка строк и столбцов
Табл.8 характеризует устойчивость упорядочения столбцов табл.3. В 100 экспериментах столбец (значение) “женат” 68 раз оставался на месте и 32 раза программа нашла ему место за столбцом “холост”. Таким образом, в экспериментах столбец “женат” был только на краю таблицы.
Значения, характеризующие разные типы неженатых, неустойчивы и в таблицах, полученных по имитированным выборкам, многократно перемещались на новые места. Это скорее всего означает, что в данном случае в упорядочении "вдовец-разведен-холост" не следует искать искать особого содержательного смысла (например, скрытой переменной, связанной с возрастом).
Таблица 8. Устойчивость порядка столбцов табл.3 (значений перем.
“Семейное положение”)
|
Столбцы,
за которые |
Перемещаемые
столбцы |
|||
|
происходит
перемещение |
женат |
вдовец
|
разведен |
холост
|
|
женат |
68* |
0 |
14
|
8 |
|
вдовец |
0 |
60* |
0
|
27 |
|
разведен |
0 |
6 |
61* |
0 |
|
холост |
32 |
34 |
25
|
65* |
|
Перед
столбцом “женат” |
0 |
0 |
0
|
0 |
Черно-белый анализ связи переменных
Необъятность таблиц
стимулировала появление множества методов исследования таблиц сопряженности
[14, 20, 21]. Эти методы позволяют выявить соответствия и даже провести
оцифровку значений переменных, но оставляет за исследователем работу по
интерпретации шкал.
Предлагаемый в данной
работе метод предназначен для автоматизации быстрого обнаружения основных
тенденций связи пары переменных. Исходными данными для анализа является
совокупность объектов, описанных двумя переменными X и Y. Метод состоит в поиске
такого дихотомического ("черно-белого") разбиения значений этих
переменных, чтобы четырехклеточная таблица сопряженности агрегированных
переменных была максимально контрастной. Мы пытаемся разделить совокупность по
каждой из участвующих переменных на 2 группы, отражающие два полюса в значениях
переменных - “черное-белое”, "богатые-бедные",
"старые-молодые", "должности прибыльные-неприбыльные";
группировка происходит одновременно по двум переменным. Исследование
устойчивости позволяет выявить нечеткость соответствия значений переменной
полюсам. Преимущество, к которому мы стремимся - это простота интерпретации.
Дихотомия для разных типов шкал
Пусть значениям
переменной X (или Y) соответствует разбиение
совокупности объектов на непересекающиеся классы объектов r={r1,...,rl}.
Дихотомическое группирование состоит в объединении этих классов в разбиение R={R0,R1}.
Достаточно определить только одну группу значений переменной, которым
соответствует класс R0, класс R1 составят остальные объекты.
Значения номинальной
переменной не упорядочены, поэтому группировка по ней не подчиняется какому
либо правилу: R0=
, где T может быть любым подмножеством
множества {1,...,l}.
При группировании
значений ранговых и количественных переменных целесообразно объединять только
группы рядом стоящих значений - интервалировать, поэтому R0= 
, где T={i| 
}.
Особый класс представляют
собой переменные, имеющие "кольцевую" структуру множества значений:
наименьшее и наибольшее значение считаются совпадающими или близкими [22].
Примером таких переменных
может служить время суток: 0 часов совпадают с 24 часами. Вторым примером может
быть возраст индивидуума, рассмотренный с точки зрения возможности их привлечения
к общественному труду. Глубокие старики и малые дети с этой точки зрения
одинаково бесполезны. Здесь целесообразно в качестве R1 брать
интервал значений, в общем случае не начинающийся с первого значения R0
=
, где T =
{i| 
}.
Критерий дихотомического группирования.
Контрастность таблицы.
Пусть значения каждой из
переменных X и Y сгруппированы в два класса и представлены разбиениями Rx
и Ry.
Для исследования значимости связи Rx и Ry изучается
таблица частот ||Fij||,
i=0..1,
j=0..1, в которой индексы i и j соответствуют классам Rx
и Ry.
Существует множество
коэффициентов, характеризующих связь дихотомических переменных: перекрестное
отношение, коэффициент Юла, коэффициент коллигации и др.
[23]; целесообразно использовать и описанные выше Z-статистики отклонения
частот (достаточно взять отклонение F00). Однако мы
воспользовались более простым показателем и эффективным с точки зрения
алгоритма оптимизации - смещением элемента F00 от его ожидаемого в
условиях независимости значения E00.
Устойчивость и полутона в черно-белом
анализе
При работе алгоритма
"черно-белого" анализа на сгенерированных данных часть значений
класса Rx0 перейдет в Rx1 и наоборот, часть
значений класса Rx1 перейдет в Rx0. То же самое касается
классификации по Y.
В результате
экспериментов каждому значения переменных X (Y) приписывается
относительная частота, с которой значение оказывалось в классе Rx1
(Ry1). Совокупность таких относительных частот может
быть также выражена средним индикаторных векторов Ix и Iy,
получаемых в экспериментах. Образно выражаясь, значения переменной X
(Y), во всех экспериментах попавшие в нулевой класс -
"черные", значения всегда попадающие в первый класс -
"белые", значения, для которых соответствующая относительная частота
между нулем и единицей - "полутона".
Пример. Профессиональная подготовка и душевой доход.
Здесь мы рассмотрим совместную группировку по
переменной “Профессиональная подготовка”, рассматриваемой как номинальная и по
количественной переменной “душевой доход” (данные 1993г.).
Группировка по
профессиональному образованию, полученной с помощью рассматриваемого метода,
имеет следующий вид. Класс 0: "нет профессионального образования",
"курсы", "ПТУ, ФЗУ, РУ"; класс 1: "среднее
специальное", "высшее", "другое".
Группировка по душевому
доходу представлена интервалами. Класс 0: менее 4500 руб.; класс 1: не менее
4500 руб.
Таким образом,
профессиональное образование представлено “полюсами”: “низкий-высокий” уровень
образования; доходы -”полюсами”: “низкие-высокие” доходы (табл.9).
В ячейке (“низкий доход”,
“низкий уровень образования”) удалось добиться смещения частоты равного 79.4.
Содержательно можно сделать вывод, что высокий уровень образования дает больше
возможностей улучшить состояние семейного бюджета.
Таблица 9. Связь профессионального образования с душевым доходом (абсолютные частоты, проценты по строке и по столбцу)
┌──────────────┬────────────────────────────────────┐
│Душевой
│ Профессиональное образование │
│доход ├─────────────┬─────────────┬────────┤
│
│Низкий │
Высокий │ Всего │
│
│уровень │
уровень │ │
│
│образования │
образования │ │
├──────────────╔(00)═════════╦(01)═════════╗────────┤
│Низкий духод
║ 405 ║ 203 ║ 608
│
│(менее 4500)
║ 66.6% ║
33.4% ║ 57.6%│
│
║ 71.7% ║
41.4% ║ │
├──────────────╠(10)═════════╬(11)═════════╣────────┤
│Высокий доход ║ 160 ║ 287
║ 447
│
│(не менее
║ 35.8% ║
64.2% ║ 42.4%│
│ 4500)
║ 28.3% ║
68.6% ║ │
├──────────────╚═════════════╩═════════════╝────────┤
│ Всего
│ 565 │ 490 │ 1055
│
│
│ 58.6% │ 41.4% │
100.0%│
└──────────────┴─────────────┴─────────────┴────────┘
Таблица 10. Устойчивость классификации по проф.образованию.
┌────────────────┬────────────┬────────────┬────────────┐
│Проф.образование│ курсы │
ПТУ, │ нет проф. │
│
│ │ ФЗУ, РУ
│ образования│
├────────────────┼────────────┼────────────┼────────────┤
│Степень серости │ 0% │ 4%
│ 14% │
├────────────────┼────────────┼────────────┼────────────┤
│Проф.образование│ высшее
│среднее │
другое │
│
│
│специальное │
│
├────────────────┼────────────┼────────────┼────────────┤
│Степень серости │ 87% │ 100%
│ 100% │
└────────────────┴────────────┴────────────┴────────────┘
Таблица 11. Устойчивость классификации по душевому доходу.
┌───────────────┬──────────────────────────────────────────────────────┐
│Душевой
доход │менее 3600 3600 3700 3725 3800 3900 4050 4100
4109 │
│Степень
серости│ 0% 6%
8% 10% 15% 21%
43% 58% 58%
│
├───────────────┼──────────────────────────────────────────────────────┤
│Душевой
доход │ 4109 4118 4150 4200 4230 4250 4300 4350 4400 4450 │
│Степень
серости│ 58% 58%
58% 58% 58%
60% 60% 65%
70% 77% │
├───────────────┼──────────────────────────────────────────────────────┤
│Душевой
доход │ 4500 4530 4600
4750 4900 5000
более 5000 │
│Степень
серости│ 91% 91%
93% 94% 95%
100% 100% │
└───────────────┴──────────────────────────────────────────────────────┘
Устойчивость классификации по профессиональному образованию показана в табл.10, в которой графа "Степень серости" соответствует частоте попадания значений в класс 1. Классификация недостаточно надежна в отношении группы не имеющих профессионального образования (возможно это молодежь, способная активно зарабатывать уличной торговлей, процветающей в год проведения обследования), неустойчиво классифицируется группа с высшим образованием (вероятно из-за несоответствия опыта прежней работы современным условиям). Первая - 14 раз оказывалась в классе 1, вторая - 13 раз в классе 0.
Устойчивость
классификации по душевому доходу
представлена в табл.11. Граница, разделяющая классы принимала в
экспериментах значения от 3600 до 5000.
Неальтернативные вопросы
При анализе
неальтернативных вопросов в качестве объекта (статистического наблюдения)
рассматривается пара ответов. Переменные считаются номинальными. Опыт показал,
что техника анализа здесь такая же, как в обычном случае.
АВТОМАТИЗАЦИЯ ТИПОЛОГИЧЕСКОГО ГРУППИРОВАНИЯ
Типологией называется логическое разделение
совокупности объектов на качественно различные группы объектов - типы [24].
В соответствии с таким пониманием типологии мы
рассматриваем множество целевых переменных, по которым оценивается качество
группирования, и множество группировочных переменных, используемых для
построения логики группирования. Таким образом, основная идея автоматизации
типологического группирования заключена в рабочей формуле:
Типология
= Логика Группирования + Цель Группирования
Формальной целью группирования является разделение
совокупности объектов (анкет) на классы, различающихся по множеству
"зависимых" переменных 
; для формирования логики группирования используется
множество "независимых" переменных 
.
Типология здесь -
разбиение 
совокупности объектов на классы (типы), оптимальное с точки
зрения его связи с целевыми переменными Y, построенное с использованием
логики группирования объектов по множеству "независимых" переменных X.
При построении классификации R мы ограничиваем сложность логики
группирования формальными критериями (число вершин в дереве группирования,
число типов, размер групп и т.п.) или, при построении типологии в диалоговом
режиме, интуитивно.
Критерий построения классификации
В качестве критерия
классификации (типологии) мы используем
внутриклассовый разброс, как это делается в ряде алгоритмов кластерного анализа
[15], однако здесь используется модификация критерия, позволяющая работать как
с количественными, так и с неколичественными переменными. Таким критерием
является критерий: 
, где D(Yk,R) - коэффициент
детерминации для количественных Yk и коэффициент Валлиса
[25] для неколичеcтвенных Yk. Для количественной
переменной Y минимизация внутриклассового разброса по множеству допустимых
разбиений R эквивалентна максимизации коэффициента детерминации D(Y,R);
коэффициент Валлиса является обобщением коэффициента детерминации для
номинальных переменных Y.
Конструирование типологии.
При формулировании логики группирования мы идем
простого к сложному. Вначале сформулируем
типы группирования по отдельным
переменным, затем по множеству переменных.
Одномерное группирование. Пусть значениям переменной X соответствует
разбиение совокупности объектов на непересекающиеся классы объектов - 
. Одномерное группирование состоит в объединении этих классов
в разбиение 
.
Значения номинальной
переменной не упорядочены, поэтому группировка по номинальной переменной не
подчиняется какому либо правилу классы Ri могут быть
объединением любого подмножества классов r.
При группировании
значений ранговых или количественных переменных целесообразно объединять только
группы рядом стоящих значений - интервалировать. Нами предусмотрен, также
специальный подход к группированию ранговых переменных с неопределенными
значениями, ранг которых не определен. Эти значения могут быть приписаны к
любому интервалу значений.
Многомерная типология. Анализ
и синтез типов. В многомерном группировании многократно используются
одномерное группирование. Группирование происходит в два этапа.
Первый этап, - анализ - состоит в последовательном
разбиении совокупности объектов по признакам. Прежде всего по каждому из
"независимых" признаков 
ищется оптимальная с
точки зрения критерия группировка объектов и "лучшая" среди этих
группировок берется в качестве начального приближения типологии 
. При этом для каждого признака рассчитывается доля
объясненной группировкой дисперсии целевых (зависимых) переменных, что и служит
основанием выбора "лучшего" разбиения 
На следующем шаге выбирается
"оптимальная" с точки зрения критерия пара - один из классов полученного
разбиения и один из признаков, по которому происходит группировка объектов
этого класса и получается группировка 
. Далее процедура повторяется и получаются классификации 
, 
... и т.д.
Процесс идет до тех пор, пока исследователь не
решит, что полученный результат удовлетворяет его по полноте описания связи
систем переменных, либо дерево группирования достигает заранее заданного числа
вершин.
Второй этап - синтез
- состоит в объединении полученных на первом этапе групп. Полученная
группировка рассматривается как переменная, из которой нужно построить
группировку с меньшим (заданным) числом классов, оптимизируя все тот же
критерий (точнее, минимизируя потерю в результате объединения доли объясненной
на этапе разбиения дисперсии).
Характеристики устойчивости
Оценка устойчивости группировки делается с
использованием тех же принципов, что и при анализе устойчивости классификации
методом k средних и в “черно-белом” анализе.
Рассмотрим самую простую ситуацию: строится
одномерная типология 
по переменной X.
Значениям этой переменной соответствует разбиение совокупности объектов 
, классы которого объединяются в классы разбиения R.
Таким образом, 
соответствует номер c(i)
класса R, в который входит эта группа объектов. Логика группирования
объектов генерированной выборки, построенная по образцу исходной типологии R,
в ситуации неустойчивости становится неоптимальной. Мы "улучшаем"
группировку на генерированной выборке путем перемещения групп объектов из
класса в класс, выходя на локальный оптимум по “объясненной” дисперсии. При
этом сохраняется соответствие между классами разбиения R исходных данных и
классами разбиения сгенерированных данных и можно считать, что в результате
случайного "возмущения" группы разбиения r "переместились"
из класса в класс разбиения R.
Естественно считать, что одномерная типология
устойчива, если при повторном сборе данных логика объединения групп остается
прежней - не происходит смены номеров классов c(i), i=1,...l. Группы,
часто меняющие номера классов c(i), естественно считать
неустойчивыми.
Обозначим f(i) частоту, с которой на
сгенерированных выборках менялись номера классов c(i). Назовем неустойчивостью
группы 
относительную частоту
смены классов c(i),
где f
- общее число экспериментов. Соответственно устойчивость группы
характеризуется величиной St(i)=1-p(i).
Итак, устойчивостью группировки по переменной
называется взвешенная с весами w(i) сумма устойчивостей групп: 
, где w(i)- суммарный вес элементов
группы.
Пример. Устойчивость в одномерном группировании
В качестве иллюстрации проверки устойчивости
группировки по одной переменной рассмотрим результаты 20 экспериментов по
анализу устойчивости группировки должностей (табл.12). Целевыми признаками
группирования были оценки респондентов, являются или не являются необходимыми
для преуспевания трудолюбие, честность, ответственность, предприимчивость -
дихотомические переменные, соответствующие деловым качествам, включенным в
число подсказок вопроса о качествах, необходимых для преуспевания.
Таблица
12.
Разбиение на группы
значений признака
"Должность".
|
Должность |
Вес |
Устойчивость |
|
Тип 1: |
78 |
87% |
|
руководитель |
38 |
100% |
|
служащий |
40 |
75% |
|
Тип 2: |
437 |
95% |
|
специалист |
95 |
95% |
|
кв.рабочий |
82 |
100% |
|
некв.рабочий |
38 |
85% |
|
част.
предпр. |
12 |
75% |
|
нет раб. |
210 |
95% |
Причина неустойчивости состоит, по видимому, в
нечеткой выраженности связи значений целевых и группируемых переменных.
Устойчивость в многомерном группировании
Устойчивость группирования в процессе
последовательного разбиения проверяется в точном соответствии с описанным
способом; отличие в том, что характеристика устойчивости переменных вычисляется
на совокупностях, соответствующих вершинам - кандидатам на разбиение.
Устойчивость синтеза типов - это устойчивость
группирования переменной, соответствующей висячим вершинам дерева
группирования.
Для демонстрации дерева
группирования с характеристиками устойчивости воспользуемся типологией,
построенной по переменным "Пол", "Возраст", "Семейное
положение" и "Образование", с целью выяснения, какую группу населения
больше волнуют такие ценности как "Семья" и "Будущее детей"
(рис.3). Целевые признаки
"Семья" и "Будущее детей" представлены дихотомическими
переменными. Хотя признак возраст принимал участие "в конкурсе"
переменных для группирования данных, он не участвовал в логике группирования.
Первый шаг разбиения в этой типологии характеризуется полной стабильностью: в информации о нулевой группе сразу после сведений об объясненном приросте (12.18%) указана устойчивость разбиения, равная 1.00. Разбиение группы 1 (преимущественно женатых (замужних)) по образованию менее стабильно и составляет всего 0.83. Табл.13 дает более полное представление об устойчивости этого разбиения.
Рис.3. Типология населения по ориентации на семейные ценности. Структура строки рисунка: номер группы, символ “<“, если группа разбивается, символ “*” с последующим за ним номером типа, если группа представляет висячую вершину; описание вершины (группы): число объектов (вес), в скобках вида “<.>“ - доля объясненной дисперсии, устойчивость последующего разбиения, переменная и список значений, ее идентифицирующих.
|
Группа Тип |
|
|
||||
|
0< |
*515
<12.18%1.00> |
|
||||
|
1< |
|
330:1.00
<2.17%0.83> Сем.положен: SYSMISS..женат |
||||
|
4*3 |
|
|
51:1.00
<2.14%0.82> Образов.:неполн.ср. |
|||
|
5*3 |
|
|
81:0.64
<0.69%0.75> Образов.:общ.ср..пр.-техн. |
|||
|
6*2 |
|
|
198.0:0.86
<0.96%0.70> Образов.:ср.спец..высш. |
|||
|
2< |
|
104:1.00
<2.13%1.00> Сем.положен:развед..вдов |
||||
|
7*1 |
|
|
15:1.00
<0.51%0.64> Пол: мужской |
|||
|
8*3 |
|
|
89:1.00
<0.98%0.65> Пол: женский |
|||
|
3*1 |
|
81:1.00
<1.18%0.86> Сем. полож.:холост(незамужем) |
||||
Таблица 13. Устойчивость
второго шага разбиения. Группа 1 разбита по признаку "Образование".
Устойчивость 82.70%.
|
образование |
Вес |
Устойчивость |
|
Группа 4: |
51 |
100% |
|
неполное среднее |
51 |
100% |
|
Группа 5: |
81 |
64% |
|
общее среднее |
44 |
50% |
|
профессионально-техническое |
37 |
80% |
|
Группа 6: |
198 |
86% |
|
среднее специальное |
79 |
80% |
|
высшее |
119 |
90% |
Как следует из информации о группе 2 (рис.3),
третий шаг разбиения устойчив. Это естественно, поскольку при разбиении по полу и нет других вариантов, кроме
разбиения на два класса.
Информация об устойчивости синтеза типов аналогична информации об устойчивости разбиений групп
(табл.14).
Таблица 14. Синтез типов, устойчивость равна 96.32%
|
Группа(1..8) |
Вес |
Устойчивость |
|
Тип 1: |
96 |
100% |
|
Группа 3 |
81 |
100% |
|
Группа 7 |
15 |
100% |
|
Тип 2: |
198 |
100% |
|
Группа 6 |
198 |
100% |
|
Тип 3: |
221 |
91% |
|
Группа 4 |
51 |
95% |
|
Группа 5 |
82 |
80% |
|
Группа 8 |
88 |
100% |
Для полноты восприятия картины группирования
представим таблицу процентного распределения целевых переменных (табл.15). Тип
1, тип не отдающий предпочтения семейным ценностям, (17.7% ценят будущее детей,
31.2% - семью) - холостые (незамужние) и вдовые и разведенные мужчины -
полностью устойчив по отношению к синтезу типов. Тип 2, ценители семьи и детей
(соответствующие цифры - 78.3% и 72.7%) - женатое, относительно высоко
образованное население - также устойчив на 100 процентов. Тип 3, промежуточный
тип (69.2% и 47.1%) - невысоко образованные женатые (замужние), а также
разведенные и вдовые респонденты - устойчив на 91%. Наименее устойчива группа 5
- женатые, имеющие среднее и профессионально-техническое образование. В ней
относительно высока доля ценителей семьи (56.1%), что приближает их ко второму
типу. По видимому, второе обстоятельство является причиной того, что эта группа
в 20 экспериментах 4 раза уходила из типа 3.
Таблица 15. Доли в типах и группах респондентов (%), отметивших среди ценностей
будущее детей и семью
|
|
Будущее
детей |
Семья |
Вес |
|
Тип
1 |
17.7 |
31.2 |
96 |
|
Группа
3 |
18.5 |
32.1 |
81 |
|
Группа
7 |
13.3 |
26.7 |
15 |
|
Тип
2 |
78.3 |
72.7 |
198 |
|
Группа
6 |
78.3 |
72.7 |
198 |
|
Тип
3 |
69.2 |
47.1 |
221 |
|
Группа
4 |
58.8 |
45.1 |
51 |
|
Группа
5 |
68.3 |
56.1 |
82 |
|
Группа 8 |
76.1
|
39.8
|
88 |
К сожалению, процедура проверки устойчивости
разбиений локальна, касается только группировки объектов по отдельным
переменным. Проверка устойчивости выбора переменных на шаге группирования и
устойчивости дерева группирования в целом пока слишком трудоемка и требует
много машинного времени. Поэтому решение этой задачи - в будущем.
Перспективы и проблемы
Представленное изложение
имело целью продемонстрировать, как описанные методы исследования устойчивости
обогащают весьма широкий спектр алгоритмов исследования данных и могут
применяться при простом исследования значимости связи, в кластерном анализе, в
задачах построения типологий и др. Естественность процедуры имитации сбора
данных, простота и ясность метода делает, на наш взгляд, его понятным людям, не
искушенным в методах обработки данных.
Имитация данных может
быть основана не только на выборке с возвращением, но и на перемешивании. Она
полезна для исследования независимости, частности и для решения ранее
разрешимой только в достаточно простых случаях проблемы множественных
сравнений. Эта задача была предметом “соревнования” многих статистиков при
сравнении средних в одномерном дисперсионном анализе. Наш опыт здесь состоит в
сравнениях групп в детерминационном анализе, основанном на простых статистиках
[26] и эту область предстоит расширить.
Огромная потребность
имеется в типологизации временных рядов. Здесь стоит проблема исследования как
устойчивости результатов типологизации, так и прогноза. Здесь для иследовния
границ изменения процессов и их устойчивости полезны выборка с возвращением и
перемешивание данных.
Хотя метод моделирования
данных представляет мощный инструмент анализа данных, в основе его лежит
жесткое предположение о репрезентативности выборки. Доказательство
репрезентативности - сложная задача и, к сожалению она остается существенной
методологической и практической проблемой.
Выборка с возвращением с
использованием ранее назначенных весов все-же не может считаться полноценной
имитацией сбора данных, поскольку весовые коэффициенты обычно корректируются по
собранным данным, а значит нужно определять веса генерированных данных.
Таковы, коротко, проблемы
и перспективы указанного круга исследований.
Литература
1. Айвазян С.А., Енюков
И.С., Мешалкин Л.Д. Основы моделирования и первичная обработка данных/ М.:
Финансы и статистика, 1983.
2. Петрович М.П.,
Давидович М.И. Статистическое оценивание и проверка гипотез на ЭВМ. М., Финансы
и статистика,1989.
3. Иберла К. Факторный
анализ/ М.: Статистика, 1980. 398 с.
4. Шеффе Г. Дисперсионный
анализ. М.: 1963
5. Exact statistics. Документация
к статистическому пакету SPSS. Чикаго, 1996
6. Ермаков С.М., Михайлов
Г.А. Статистическое моделирование. М., Наука, 1982
7. Efron B. Better bootstrap confidence intervals.//J. Amer. Statist.
Ass., 81, 1986.
8. Эфрон Б.
Нетрадиционные методы многомерного
статистического анализа/ М.: Финансы и статистика, 1988.
9. Gray H.L., Schukanu W.R. the generalized jacknife statistics.- N.Y.:
Marcel Decker, 1972.
10. Ростовцев П.С.,
Костин В.С. Автоматизация типологического группирования // Препринт 137, ИЭиОПП
СО РАН, Новосибирск, 1995
11. Ростовцев П.С.
Черно-белый анализ связи переменных/ Анализ и моделирование экономических
процессов переходного периода в Россиию-Новосибирск: ЭКОР, 1996.- с. 264-284.
12. Ростовцев П.С.
Значимость и устойчивость автоматической классификации - возможности
исследования при анализе археологических данных / Методы естественных наук в
археологических реконструкциях. - Новосибирск: 1995. с. 59-68.
13. Ростовцев П.С.,
Смирнова Н.Ю., Корнюхин Ю.Г., Костин В.С.
Анализ таблиц сопряженности неальтернативных признаков // Препринт 138,
ИЭиОПП СО РАН, Новосибирск, 1995
14. Аптон Г. Анализ
таблиц сопряженности/ М.: Финансы и статистика, 1982. 143 с.
15. Дюран Б., Оделл П.
Кластерный анализ/ М.: ИЛ, 1977.
16. Hartigan J.A. Clustering algorithms/ Wiley. N.Y., 1975.
17. Браверман Э.М.,
Мучник И.Б. Структурные методы обработки эмпирических данных./ M., Наука, 1983.
18. Bock H.H. On some significance tests in cluster analysis // Journal
of Classification, 1985. N1,
77-108.
19. Майника Э. Алгоритмы
оптимизации на сетях и графах/ М.: Мир,
1983
20. Жамбю М.
Иерархический кластерный анализ и
соответствия/, Финансы и статистика, 1988.
21. Енюков И.С. Методы,
алгоритмы, программы многомерного статистического анализа/ М.: Финансы и
статистика, 1986, 232 с.
22. Лбов Г.С. Методы
обработки разнотипных экспериментальных данных/ Новосибирск:
Наука, 1981. 1983.
23. Флейс Дж.
Статистические методы для изучения таблиц долей и пропорций/ М.: Финансы и
статистика, 1989.
24. Плошко Б.Г. Группировка и системы
статистических показателей/ М.: Статистика, 1971. 176 с.
25. Миркин Б.Г. Анализ
качественных данных и структур./ М.:,
Статистика, 1980.
26. Ростовцев П.С. Статистические характеристики детерминации // Статистическое моделирование экономических процессов/
Новосибирск, Наука, 1991.