П.С. Ростовцев, В.С. Костин

К вопросу о структуре распределения

Аннотация

Гистограмма распределения непрерывной переменной представляет собой “частокол”, по которому сложно представить себе качественную структуру распределения генеральной совокупности - число локальных максимумов, промежутки высокой и низкой плотности, что важно при исследовании социально- экономических данных. Провести анализ качественной структуры совокупности можно, группируя данные. В этом случае многое зависит от выбранного шага группирования - необходимо найти компромисс между точностью изображения данных и наглядностью. С точки зрения “правильного” представления данных целесообразен выбор неравномерных интервалов и представление данных в виде “правильной” гистограммы - полиграммы.

В отличие от известных методов непосредственного восстановления плотности, использующих парзеновских окна, и схем восстановления плотности, предлагаемых Вапником [1], мы пользуемся аппроксимацией функции распределения в пределах доверительного шнура, построенного по эмпирической функции распределения.

Введение

В 1997 году мы под руководством П.С. Ростовцева занимались разработкой программы “Camel”, основанной на идее, описанной в этом тексте. Программа была реализована и применяется до сих пор, а теоретическое описание при жизни Петра Симоновича было опубликовано лишь в кратких тезисах доклада [2]. В настоящее время появились планы продолжения этой работы, и возникла необходимость в публикации полного текста статьи.

Получение одномерных распределений - это первый этап исследования собранных эмпирических данных социально-экономических исследований. В статьях, отчетах представляемых потребителям информации (учреждениям административного управления, коммерческим организациям, средствам массовой информации) используется наглядное изображение информации - гистограммы, различного рода диаграммы. Для адекватного изображения распределения непрерывной переменной в виде гистограммы важно правильно выбрать такой шаг группирования наблюдений, чтобы, с одной стороны, не потерять основные элементы структуры (промежутки высокой и низкой плотности) и, с другой стороны, не отражать в графике случайные элементы, которые при повторном сборе информации могут исчезнуть.

Пример 1. Длительность сна.

Приведем пример распределения непрерывной случайной величины. Для этого рассмотрим данные летнего обследования бюджетов времени трудоспособного населения сельского хозяйства. Эти данные были получены в рамках анкетного обследования сельского населения (Институт экономики и организации промышленного производства СО РАН), объем выборки 250 человек. При сборе данных в числе прочей информации в специально разработанных анкетах с точностью до пяти минут фиксировались ответы респондентов о времени и длительность различных видов деятельности сельского населения. Для иллюстрации метода мы возьмем лишь одну переменную - суммарное время сна респондента.

Гистограмма распределения числа респондентов по времени сна приведена на рис.1. В ней предусмотрен 15-минутный шаг группирования значений изучаемой переменной. Это распределение будет использовано для построения диаграмм - иллюстраций в дальнейшем изложении предлагаемых методов.

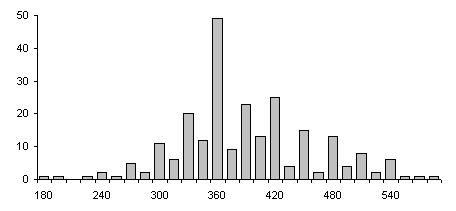
Рис.1. Распределение числа респондентов по длительности сна.

Рассматривая распределение, мы видим множество пиков - локальных максимумов, связанных со склонностью респондентов округлять свои ответы до определенной точности - почти регулярно с получасовой периодичностью высокие столбцы гистограммы чередуются с низкими. Возможно, это связано не только с желанием округлять временные значения. но и с режимом сна, который задает себе респондент. При более подробном рассмотрении исходных данных наблюдалась также 15-минутная периодичность локальных максимумов. Возникают вопросы:

- насколько существенно такое негладкое поведение распределения?

- какой интервал группирования был бы здесь приемлем?

- может быть, более адекватным здесь будет выбор неравномерных интервалов группирования с соответствующим изображением диаграммы распределения?

- насколько возможно гладкое представление плотности?

Доверительные границы для функции распределения

Воспользуемся общепринятыми обозначениями:

t₁...t_n - выборка (реализации одинаково распределенных независимых случайных величин);

z₁....z_m - вариационный ряд - неповторяющиеся значения t_i , упорядоченные в порядке возрастания;

n₁...n_m - частоты повторения значений z_i ();

- эмпирическая функция распределения

В частности, в нашем примере z - длительность сна i-го респондента. В гистограмме распределения значения z_i берутся с точностью до шага группирования данных. В общей статистике значения функции распределения для выражения в процентах иногда домножают на 100 и называют накопленными относительными частотами.

Теоретической функцией распределения случайной величины x называют функцию F(t)=Prob{x£t} - вероятность того, что x будет не больше t.

Доверительные границы по Колмогорову-Смирнову. Одним из наиболее популярных тестов для проверки гипотезы того, что выборка произведена из совокупности, имеющей распределение x, является критерий Колмогорова-Смирнова[3]: . Теоретическая функция распределения критерия Колмогорова-Смирнова на больших выборках приближенно выражается следующим образом:

Впрочем, для малой выборки используются другие апрроксимации теоретической функции распределения KS.

Благодаря обращению функции распределения KS можно определить границы по отношению к F(t), выход за которые теоретической функции распределения F^*(t) маловероятен. Соответственно по эмпирическим данным можно установить границы, в которых должна находится теоретическая функция распределения, для которой соответствующие значения эмпирической функции распределения не будут маловероятны. Эти границы определяются предварительным заданием вероятности отклонения (значимости) a, нахождением критических точек с помощью решения уравнения и получением значения отклонения, равного . Величина b=1-a называется также доверительной вероятностью.

В частности, значение , отсюда в нашем примере отклонение эмпирической функции распределения от теоретической функции распределения на величину возможно только с вероятностью 0.05. На рис.2 представлена эмпирическая функция распределения и доверительные границы Колмогорова-Смирнова для теоретической функции распределения, полученные при уровне значимости 0.05.

Заметим, что график выполнен нетрадиционным способом. Для демонстрации непрерывности переменной мы отказались от изображения эмпирической функции распределения в виде ступенчатой функции - мы просто соединили ломаной точки (z_i,F^*(z_i)) . Доверительные границы вычислялись также только в точках z_i и также были соединены ломаной.

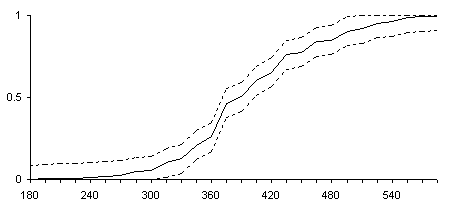
Рис.2. Доверительные границы Колмогорова-Смирнова.

Поточечные доверительные границы. Заметим, что величина F^*(t) представляет собой долю статистических испытаний, в которых значение x оказалось не больше t, а k=nF^*(z_i) - число таких испытаний. Обозначим p=F(t)=Prob{x£t}. В таких обозначениях величина k имеет биномиальное распределение с параметрами p и n (). Доверительные границы двустороннего доверительного интервала для p получаются решением уравнений

(1)

(2)

Поскольку такие доверительные границы определяются для F(t) в каждой точке t, мы называем эти границы поточечными. Ширина доверительного интервала здесь зависит от величины F^*(t). Самый широкий интервал получается при F^*(t)=0.5, Решение указанных выше уравнений на большой выборке связано с вычислительными сложностями. Поэтому для большой выборки необходимо применить нормальное приближение для биномиального распределения и найти корни относительно p уравнения:

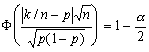(3)

Как известно, в случае, когда значение F^*(t) приближается к нулю или единице, вместо нормального приближения рекомендуется использовать приближение Пуассона. В данном случае неизвестна оптимальная граница перехода от нормальной аппроксимации к аппроксимации Пуассона, и нас утешает то, что эксперименты на реальных данных с формальным применением нормальной аппроксимации показали приемлемые результаты: представленные на графиках границы, полученные разными способами на выборках объема свыше 200 объектов, практически сливаются. На рис.3 представлены поточечные доверительные границы, полученные при уровне значимости 0.05, для тех же данных о продолжительности сна.

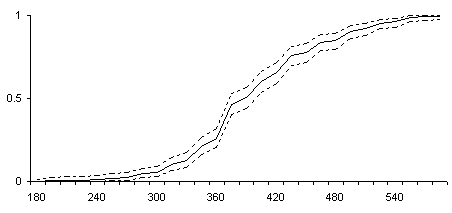
Рис.3. Поточечные доверительные границы функции распределения.

Поточечные доверительные границы уже, чем границы Колмогорова-Смирнова. В частности, вблизи медианы (F^*(375)=0.504) поточечные границы равны 0.436 и 0.569, а границы Колмогорова-Смирнова равны 0.416 и 0.592.

Еще раз обратим внимание на отличие указанных двух видов интервалов: границы Колмогорова-Смирнова “ловят” всю теоретическую функцию распределения с вероятностью 1‑a, а поточечные границы - с этой вероятностью “ловят” значении F(t) при любом заранее фиксированном значении t.

Доверительные границы и структура распределения

Чем шире доверительные границы, тем проще выводы о распределении. При широком доверительном интервале в полученные границы можно вписать отрезок прямой, который соединит ось t и прямую y=1, а это показывает, что распределение может быть простейшим равномерным распределением. Узкие границы, скорее всего, не позволят вписать в доверительные границы столь простую теоретическую функцию распределения.

Ширина доверительного шнура зависит от объема выборки: чем больше выборка при фиксированном уровне значимости, тем уже доверительный шнур. Это естественно, поскольку большая выборка дает больше информации и более тонкие сведения о теоретическом распределении.

Изменение уровня значимости (доверительной вероятности) также приводит к изменению ширины доверительной области. Доверительный коридор шире для большей доверительной вероятности (меньшего уровня значимости a): простые сведения, которые даются широкими доверительными интервалами, более надежны, и узкие границы, соответствующие малой доверительной вероятности, дают сложные, но ненадежные сведения.

Представление структуры распределения

В соответствии с изложенным выше, структуру распределения целесообразно представлять в виде теоретической функции распределения простого вида. Для этого необходимо отыскивать теоретическую функцию распределения в виде монотонной функции кусочно-линейного вида или составленную из простых полиномов второго-третьего порядка. Первый способ связан с построением особого вида диаграммы распределения - полиграммы, второй –со специального рода сплайн-функциями, обладающими изогеометрическими свойствами по отношению к функции распределения.

При поиске структуры необходимо, во-первых, находиться в рамках доверительного шнура, во-вторых, добиваться минимальной сложности структуры (числа отрезков, полиномов заданной степени), в третьих, при этих условиях добиваться минимального отличия искомой теоретической функции распределения от эмпирической функции распределения. Это достигается минимизацией функционала, используемого в критерии ω-квадрат [4]:

(4)

на заданном классе теоретических функций распределения (в зависимости от вида искомой структуры при минимальной ее сложности).

Структура распределения может быть представлена плотностью распределения, соответствующей найденным простым функциям распределения. Естественно, графики плотности будут выглядеть значительно проще и нагляднее по сравнению с гистограммой исходных данных, что позволит избежать рассмотрения несущественных деталей.

Полиграмма.

Теоретическая функция в виде ломаной соединяет отрезками прямой точки, лежашие на графике эмпирической функции распределения.

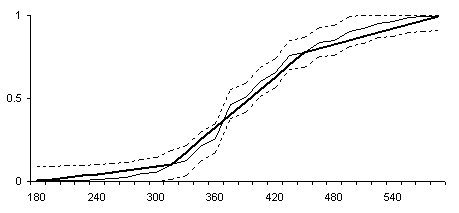
Рис.4. Представление структуры в виде ломаной в доверительных границах Колмогорова-Смирнова (a=0.05).

Функция распределения в виде ломаной соответствует переменной, плотность распределения которой равномерна на нескольких интервалах с различной плотностью распределения. График плотности распределения, соответствующей ломаной, построенной на основе эмпирической функции распределения, называется полиграммой.

График плотности распределения, построенный на основе ломаной с рис.4 будет состоять всего из 3-х прямоугольников. Детальнее структуру распределения представляют графики структуры распределения на рис. 5-6, полученные на основе поточечных доверительных интервалов (a=0.05).

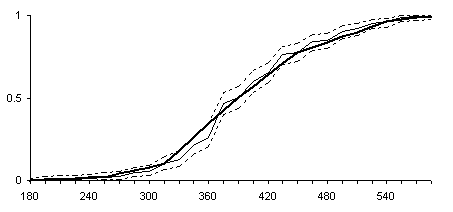
Рис.5. Представление структуры в виде ломаной в поточечных доверительных границах (a=0.05).

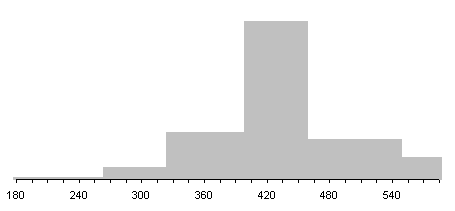
Рис.6. Полиграмма, построенная на основе поточечного доверительного интервала.

С какой вероятностью поточечный доверительный шнур “ловит” теоретическую функцию распределения?

Уровень значимости a задает область, в которой может содержаться или не содержаться теоретическая функция распределения F(t). Вопрос в том, с какой вероятностью 1-a_glob доверительный интервал накрывает F(t) целиком.

Может показаться, что соотношение a и a_glob зависит от распределения генеральной совокупности, однако, как будет показано ниже, для непрерывных распределений с ненулевой плотностью это не так.

Чтобы показать это, заметим, что применение монотонного преобразования к выборке и к генеральной совокупности, сохраняет положение теоретической функции распределения по отношению к доверительным границам: если теоретическая функция распределения не вышла из доверительного шнура, то при преобразовании она останется внутри него, и наоборот, если она не “поймана” интервалом, то и при преобразовании данных не будет им “поймана”.

Пусть g(t) - монотонно возрастающая функция, определенная для всех значений x. Рассмотрим случайную величину g(x). Реализацией выборки для нее будет совокупность значений g(t₁),...,g(t_n).

Пусть y=g(t). Очевидно, значения F_g(x)(y) и F(t) совпадают и доверительные границы для p=F_g(x)(y)=F(t) определяются на основе решения уравнений (1) и (2), где k=#{g(t_i)<y}=#{t_i<t}. Таким образом, и F_g(x)(y) и F(t) имеют одни и те же доверительные границы. Это означает, что F_g(x)(t) находится в доверительном шнуре тогда и только тогда, когда F(t) находится в доверительном шнуре.

Благодаря преобразованию g(x)=F(x), мы всегда можем получить из непрерывной случайной величины x случайную величину g(x), имеющую равномерное на интервале (0,1) распределение. Отсюда, поточечный 1-a доверительный шнур для функции любого непрерывного распределения генеральной совокупности “ловит” функцию распределения с вероятностью, с которой будет поточечным шнуром покрываться функция распределения при равномерном распределении генеральной совокупности.

Следовательно, многократно генерируя выборки из равномерного распределения, можно оценить a_glob. Рассмотрим вопрос, как это можно сделать.

Пусть выборка из равномерного распределения с параметрами (0,1) упорядочена и имеет вид t₁<...<t_k<...<t_n

Если в точке t_k оценивать доверительный интервал для p=F(t_k), то минимальная значимость, при которой истинное значение p=t_k находится на границе доверительного интервала, равна

a_k=2 min (,) .

Минимальная значимость, при которой теоретическая функция распределения не выходит за границы доверительного шнура, будет равна максимуму из этих значимостей для F(xk): a_min= max(a_k).

Фиксируем a - значимость, определяющую поточечный доверительный шнур. Поскольку доверительный шнур становится шире при уменьшении a, доверительные шнуры, построенные на эмпирических функциях распределения, для которых значимость a<a_min, и только эти доверительные шнуры, не будут содержать целиком нашу теоретическую функцию распределения.

Следовательно, доверительная вероятность 1-a_glob=Prob{a_min >a} и эмпирическая функция распределения a_min является оценкой функции, связывающей поточечную значимость a и a_glob.

Требование ненулевой плотности теоретической функции распределения необязательно, но отказ от него потребовал бы усложнить приведенные выше рассуждения.

Вычисление функции, связывающей глобальную и поточечную значимость для выборки до 100 наблюдений, происходит достаточно быстро - функция оценивается с помощью 10000 экспериментов за 5 секунд. При большем числе наблюдений вместо использования биномиального распределения используется нормальная аппроксимация.

Литература

1. Вапник В.Н. Восстановление зависимостей по эмпирическим данным. - М.: Наука, 1979. - 447с.

2. Ростовцев П.С., Костин В.С. Доверительный шнур и структура распределений// Применение многомерного статистического анализа в экономике и оценке качества продукции: Тез. докл. VI науч. конф. стран СНГ. - М.: Центральный экономико-математический институт РАН, 1997. - С. 45-46.

3. Боровков А.А. Математическая статистика. Оценка параметров. Проверка гипотез. – М.: Наука, 1984. – с. 366-367.

4. Мартынов Г.В. Критерии омега-квадрат. – М.: Наука, 1978. 80с.