П.С.Ростовцев, В.С.Костин, А.Л.Олех

Множественные сравнения в детерминационном и типологическом анализе

Исследование поддержано грантом РФФИ 98-06-80150

Введение

Парадоксально, но, изучая данные, не содержащие закономерностей, можно получить ложные заключения, которые, казалось бы, основываются на использовании статистических выводов. Особенно это относится к методам автоматизации анализа данных, в которых множество вариантов группирования, оценивается значимостью статистик. Причина здесь в том, что происходит перебор случайных значений наблюдаемых статистик.

Для пояснения ситуации приведем следующий модельный пример. Предположим, что в результате сбоя компьютера, все некогда собранные данные оказались перемешаны. Пусть исследователь, изучая связи в данных, отбирает пары переменных по уровню значимости a=0.05. При изучении 10 коэффициентов вероятность не обнаружить такого «значимого» коэффициента равна 0.9510=0.6, соответственно - вероятность найти значимую связь равна 0,4. Можно ли доверять таким результатам? По-видимому, границу значимости во множестве сравнений следует устанавливать на более высоком уровне. Она зависит от числа рассматриваемых вариантов, от связи в данных и метода, в котором возникает множество сравниваемых статистик.

Решая задачи анализа социологических данных, мы постоянно сталкивались со смещенными выборками. «Исправление» выборок происходит преимущественно за счет приписывания весов объектам. Сложность исследования статистик, с которыми нам приходится работать, особенно при анализе взвешенных выборок, делает невозможным применение традиционных методов математической статистики. Однако применение компьютерного эксперимента (метода Монте-Карло [3]) позволяет большей частью обойти эти трудности.

Проблема множественных сравнений наиболее подробно рассмотрена в однофакторном дисперсионном анализе [1,11]. Основной задачей такого анализа является сравнение средних в группах объектов. Здесь рассматривается гипотеза равенства математических ожиданий в группах объектов H0: m1=m2=…=mk, против гипотезы H1: не все матожидания совпадают. К множественным сравнениям можно также отнести использование контрастов, с помощью которых проверяют, не равна ли нулю заданная линейная комбинация матожиданий. Однако для нас наиболее интересно попарное сравнение средних в группах. Для сравнения средних (матожиданий mi и mj) групп i и j можно было бы использовать статистику Стьюдента, но из-за множественных сравнений этот подход будет недостаточно строг. Универсальным методом, применимым во многих областях статистического анализа является метод Бонферрони [12]. Пусть проводится t сравнений. Согласно методу Бонферрони, назначается уровень значимости для множественных сравнений am и для попарных сравнений порог a назначается исходя из соотношения am=1-(1-a)t. Иными словами берется оценка, возникающая при независимости средних. Возможно получение наблюдаемого значения am за счет использования наблюдаемой значимости наибольшего попарного различия. Имеется множество менее универсальных, но и менее грубых методов выбора значимо отличающихся средних, в частности, в статистическом пакете SPSS [14] множественные сравнения групп представлены 14 методами.

Если учитывать взаимосвязи в данных, задача становится очень сложной, разрешимой разве что с помощью компьютера. В данной работе мы показываем результаты применения компьютера для проведения множественных сравнений в двух методах анализа данных.

1. Анализ детерминаций

В детерминационном анализе ДА [10] рассматривается множество "независимых" признаков X={x1,…,xn} и «проблемная» группа объектов B, соответствующая значению "зависимого" признака Y=1. С точки зрения детерминации анализируются группы, соответствующие сочетаниям значений Xa: (x1,…,xn)=(a1,…,an). Обозначим N, Na, Nb и Nab - число объектов в совокупности, в группе Xa, в группе B и в пересечении Xa и B соответственно. В ДА рассматриваются две величины: I=Nab/Na – интенсивность Xa - доля объектов B в группе Xa; C=Nab/Nb - емкость Xa - доля объектов Xa в группе B. Для выбора наиболее интересных сочетаний значений признаков, задаются пороговые значения интенсивности и емкости.

Нас не удовлетворяет использование только этих статистик, так как неясна их статистическая значимость. Поэтому в дополнение к этим критериям, в работе [8] нами были использованы статистические критерии, в числе которых Z -статистика, полученная на основе точного критерия Фишера [2]. Простота метода ДА позволяет отточить технику использования различных статистик, касающихся не только дихотомических переменных Y, но и других их типов.

1.1. Z – критерий

С точки зрения детерминации интересно, насколько существенно интенсивность Xa отличается от исходной, без выделения группы по сочетанию значений X, доли объектов B. Это эквивалентно вопросу, значимо ли частота пересечения Nab отклоняется от ожидаемой в условиях независимости Xa и B величины Eab=NaNb/N ? Для измерения значимости отклонения мы используем статистику Z=(Nab - Eab)/s, где s2 - дисперсия Nab, вычисленная исходя из гипергеометрического распределения Nab. По существу, величина отклонения Nab от ожидаемой величины измеряется здесь в числе среднеквадратичных отклонений. Для больших выборок теоретическое распределение Z близко к N(0,1) - нормальному; для малых выборок Z-статистика корректируется с целью сохранения вероятностных соотношений нормального закона.

Согласно идее С.В.Чеснокова, целью является детерминация группы, и следует рассматривать только положительные смещения. Мы считаем важным обнаружение закономерностей и рассматриваем как положительные, так и отрицательные значения Z. Изучая Xa изолированно от других групп, на основании величины выборочного значения Zвыб, можно легко понять значимость отклонения Nab, тем более что программа, реализующая метод для каждой группы выдает значение вероятности P{½Z½<½Zвыб½}.

1.2. Множественные сравнения

Пусть имеется k групп Xa, для которых оценены значения ½Z½ - ½Z1½,…,½Zk½. Будем считать, что эти значения упорядочены: ½Z1½ -минимально, ½Zk½ - максимально. Как было отмечено выше, множество Z-статистик представляют собой случайные числа и даже в условиях независимости с высокой вероятностью можно случайно найти значимые величины Z. Проводя множественные сравнения, в работе [8] мы опирались на распределение максимальной статистики ½Zk½ в условиях гипотезы независимости. Наблюдаемая значимость выборочных значений ½Zi½ оценивалась вероятностью : значения статистики сравнивались с "лучшими" из случайных значений.

Если величины Nab для различных групп Xa независимы, статистики Z - непрерывны, то для вычисления значимости в смысле множественных сравнений можно использовать наблюдаемую в обычном смысле значимость . Для наблюдаемой значимостью множественных сравнений будет . Однако эта оценка груба из-за дискретности оценок Z для неизбежно малых групп Xa, взаимосвязи для этих групп статистик Z. Эта связь довольно сложна, поэтому для вычисления наблюдаемой значимости целесообразно использовать статистическое моделирование. Кроме того, такой подход позволяет работать с взвешенными выборками.

1.2.1. Статистический эксперимент

Суть эксперимента состоит в следующем. После вычисления всех статистик на заданной совокупности многократно случайно генерируются значения Y. На генерируемых выборках вычисляется величины Z - критерия. Для каждой группы подсчитывается число экспериментов, в которых максимальное значение ½Z½ (равное ½Zk½) превзойдет выборочное значение . Доля таких экспериментов и является оценкой значимости во множественных сравнениях.

Нами рассматриваются два способа моделирования зависимой переменной Y, не связанной со значениями X.

Первый способ состоит в перемешивании значений Y по объектам. Здесь сохраняются маргинальные частоты Na и Nb, что соответствует предположениям для вычисления точного критерия Фишера.

Второй способ состоит в случайной выборке с возвращением значений Y из имеющегося множества значений (метод BootStrap [13]). Здесь Nab имеет биномиальное распределение с параметрами Na и p=Nb/N. В этом случае Nab в различных группах независимы и, при невзвешенной выборке при больших N, нет необходимости проведения реального эксперимента, так как здесь может быть использован принцип Бонферрони, но вместо описанной выше статистики нужно применять статистику Z=(Nab-Np)/(Np(1-p)).

1.2.2.. Порядковые статистики и множественные сравнения

Представим себе, что мы сравниваем k=100 независимых статистик. Ориентируясь на распределение максимальной статистики ½Z100½, при пороге значимости в множественных сравнениях am=0.05, нам придется отбрасывать значения статистики, значимость которой a=1-(1-am)1/k=0,0005. При N(0,1) нормальном распределении Z критическим является значение ½Z½=3.48 ! Таким образом, ориентируясь на «лучшее» среди случайного мы так сужаем число анализируемых статистик, что для анализа практически ничего не остается.

В действительности исследователь выбирает не одну статистику, а несколько. Подозрение должны вызывать ситуации, когда среди отобранных статистик значимых столько, сколько может быть в случайных данных. Это соображение позволяет уменьшить порог значимости в множественных сравнениях.

Для установления значимости на основании этой идеи мы будем рассматривать порядковые статистики ½Zk-1½, ½Zk-2½,… и т.д. Порядковую статистику ½Zk-s½ (s=0,…,k) будем называть s-м максимумом, а s-м критическим значением порядка a - величину ½Zk-s,a½, для которой . Таким образом, ½Zk-s,a½ - значение ½Z½, больше которого случайно (в условиях гипотезы независимости) с вероятностью a может оказаться не более s значений. В условиях независимости статистик уровень значимости в множественных сравнениях по s-му максимуму и обычный уровень значимости a находятся в следующем соотношении: . Поэтому здесь также может быть использован критерий, подобный критерию Бонферрони. Некоторую сложность здесь представляет вычисление a по заданному значению , но это препятствие легко преодолимо с помощью компьютера. Вычисления показывают, что для независимых групп 5% уровню значимости по 2 и 4-му максимумам соответствуют обычные уровни значимости, равные 0.0082 и 0.02 (значения ½Z½ равны 2.33 и 2.64). Аналогично предыдущему, когда использовалось лишь распределение ½Zk½, мы оцениваем наблюдаемый уровень значимости по s-му максимуму на основании экспериментов, подсчитывая долю экспериментов, в которых значение ½Zk-s½ превзойдет выборочное значение .

1.3. Детерминация особенностей распределения с помощью критерия Колмогорова-Смирнова

В данном подходе интерес представляет не только детерминация проблемной группы, но и детерминация закономерностей. Целью здесь может быть, например, поиск групп, отличающихся средними значениями зависимых переменных, что является некоторым упрощением дисперсионного анализа, или групп с особенной конфигурацией распределения. Здесь могут использоваться статистики Стьюдента, практически любые параметрические и непараметрические критерии. Нами реализован анализ детерминации формы распределений на основе критерия Колмогорова-Смирнова [5].

В отличие от ранее рассмотренной задачи с дихотомической переменной Y, критерием здесь является значение 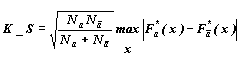, где ,а и - эмпирические функции распределения в группе объектов Xa и ее дополнении соответственно.

1.4. Пример. Анализ связи самооценки и жизненных принципов

Для анализа были взяты данные социологического обследования сельского населения Новосибирской области, проведённого ИЭиОПП СОРАН в 1997 г. (552 анкеты). В качестве изучаемой группы взята совокупность респондентов, оценивших себя как людей, собственными руками делающих свою судьбу (Nb=140 чел., 25,4% выборки). В качестве независимых переменных использованы ответы на вопрос «Какими принципами Вы предпочитаете руководствоваться в своей жизни?», содержащиеся в четырех переменных: x1 - 1-«Не выделяться», 2- «Уметь пробиваться»; x2 - 1- «Быть решительным», 2- «Уметь уступать»; x3 - 1- «Не рисковать», 2-«Не бояться нового»; x4 - 1- «Быть хорошим исполнителем», 2-«Быть лидером»; кроме того, каждая переменная содержала ответ 3-«Затрудняюсь сказать».

В результате расчётов было получено 84 группы по сочетаниям ответов, табл.1 содержит информацию о 4-х наиболее значимых группах. Было проведено 1000 экспериментов, позволивших оценить значимость в множественных сравнениях. По нулевому максимуму Z(0)=Z84 следует считать значимой лишь одну группу, показывающую очевидную связь принципов решительности, лидерства, смелости, напористости с высокой самооценкой своих возможностей (Z=4,4; ). Лишь второй максимум дал возможность оценить очевидную значимость противоположной по жизненным принципам группы (Z=-2,27; ). Третий максимум «объявляет» значимыми противоречивые третью и четвертую группы, незначимую по обычным меркам, поэтому оценка значимости по нему носит относительный характер. Таким образом, указанный метод позволил достаточно быстро и точно выбрать из исходно большого количества групп (в данном случае из 84-х) только те группы, которые действительно имеет смысл рассматривать.

Таблица 1. Группы респондентов по жизненным принципам, статистики ДА.

Незави-симые пере-менные	Уметь про-биваться	Не выделяться	Не выделяться	Уметь пробиваться
	Быть реши-тельным	Уметь уступать	Быть реши-тельным	Быть реши-тельным
	Не бояться нового	Не рисковать	Не бояться нового	Не бояться нового
	Быть лидером	Быть хорошим исполнителем	Быть хорошим исполнителем	Быть хорошим ис-полнителем
Na	23	45	35	8
Nab	17	7	16	5
I	0,74	0,16	0,46	0,63
C	0,12	0,05	0,11	0,04
Zвыб	4,4	-2,27	2,04	1,84
a	0	0,023	0,041	0,066
a(0)	0	0,325	0,37	1,84
a(1)	0	0,065	0,282	0,769
a(2)	0	0,006	0,078	0,422
a(3)	0	0	0,013	0,045

2. Типологическое группирование

Типологией называется логическое разделение совокупности объектов на качественно различные группы объектов - типы. Для автоматизации типологического группирования мы пользуемся рабочим определением:

Типология = Логика Группирования + Цель Группирования

Логику группирования мы осуществляем, конструируя классификацию объектов из множества «независимых» переменных . Целью группирования здесь является максимальное различие классов объектов по множеству "зависимых" переменных .

В работе [6] мы оценивали качество такого разбиения с помощью меры связи Q(R,Y) между разбиением R и Y. Построение типологии заключалось в иерархическом группировании совокупности объектов по переменным X. Ее оптимизация состоит в максимизации Q(R,Y). В качестве Q(R,Y) использовалась сумма коэффициентов детерминации для количественных Y и коэффициентов Валлиса для неколичественных Y. Эта сумма является обычной для кластерного анализа долей разброса Y, объясненного разбиением R.

Автоматизация группирования имеет много общего с методами построения логических решающих правил [4]. Широкую известность имеет программа Chaid [15], в которой имеется единственная зависимая переменная (номинальная или ранговая). При группировке объектов алгоритмом Chaid используется критерий значимости связи. В отличие от этих работ в данной работе целью группирования является объясненная дисперсия по множеству переменных.

В данной работе мы не имеем возможности представить полное описание алгоритма, математических и содержательных вопросов типологического анализа, поэтому затронем только ключевые моменты, касающиеся обоснованности и работоспособности метода.

2.1. Об алгоритме типологического группирования.

Если множество X состоит из единственной переменной (), конструируется одномерная типология; построение типологии состоит в оптимальном интервалировании ранговых, количественных переменных или объединении в произвольном порядке значений номинальных переменных.

В многомерном группировании многократно используются одномерное группирование. Такое группирование происходит в два этапа.

Первый этап, анализ, состоит в последовательном группировании совокупности объектов по признакам.

Прежде всего, по каждому из "независимых" признаков ищется оптимальная с точки зрения критерия группировка объектов; "лучшая" среди этих группировок берется в качестве начального приближения типологии . На следующем шаге выбирается "оптимальная" с точки зрения значимости пара (класс полученного разбиения, переменная), по которой происходит группировка объектов этого класса. В результате разбиения указанного класса по соответствующему признаку получается группировка . На следующих шагах процедура повторяется, получаются классификации ,,… и т.д. Процесс идет до тех пор, пока исследователь не решит, что полученный результат удовлетворяет полнотой описания связи X и Y, либо очередной шаг дает незначимый прирост объясненной дисперсии.

Второй этап состоит в синтезе типов - объединении классов полученной классификации в заданное или оптимальное с точки зрения значимости число классов.

2.2. Значимость при выборе переменной группирования

Будем рассматривать класс объектов, принадлежащий полученному на некотором шаге разбиению. Будем считать, что для каждой переменной из множества задан тип группирования и число классов группирования. В соответствии с целью группирования наша задача – выбрать переменную XK, по которой группировка объектов R=R(Xk)– оптимальна.

Что такое оптимальная группировка? Группирование по номинальной и ранговой переменным, переменным с различным числом значений может дать различные приросты объясненной дисперсии «зависимых» переменных. Поэтому в качестве критерия используется критерий значимости aвыб=P(Qвыб(R,Y)<Q(R,Y)}.

Для оценки aвыб производятся эксперименты по генерированию (методом BootStrap) значений переменных Y. При этом, в каждом из заранее заданного числа nexp экспериментов получается случайное значение критерия Qi=Q(R,Y) (i=1,…,nexp). Если значение Qвыб(R,Y) не превышает max(Qi), то aвыб можно оценить прямо по выборке.

Зачастую это практически невозможно. Поэтому в данной работе мы предположили, что Q(R,Y) при независимых X и Y имеет бета распределение. Основанием для такого предположения послужили результаты исследования алгоритма кластерного анализа на одно-кластерной структуре [7], в котором многочисленные статистические эксперименты показали незначимое отличие распределения Q(R,Y) от бета распределения.

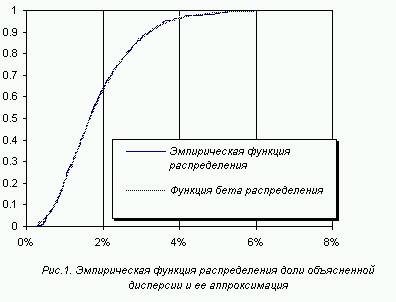
Проверка на реальных данных также показала ту же закономерность. На рис.1 показаны эмпирическая и оцененная в результате 1000 перемешиваний данных функции распределения (обследование сельского населения 1994 г., проведенное ИЭиОПП СО РАН, 512 респондентов). В этом примере исследовалась связь индикатора наличия у респондента жизненной ценности “будущее детей” с группировкой по возрасту. График показывает, что эмпирическая и теоретическая функции распределения практически неразличимы.

Известно, что бета распределение связано с распределениями Фишера, биномиальным, гамма распределением, равномерным [9] и весьма гибко меняет форму, связанную всего с двумя параметрами. Безусловно, сделанный нами выбор класса распределений – эвристика, однако опыт показывает – это неплохая эвристика. В дальнейшем она может быть уточнена и в большей степени обоснована.

Оценка параметров распределения происходит следующим образом. На основе полученной выборки {Qi} оцениваются математическое ожидание и дисперсия Q, по которым оцениваются параметры бета распределения u и w. После этого не составляет проблему вычислить aвыб=P(Qвыб(R,Y)<Beta(u,w)}.

Проверка алгоритма на реальных данных показала, что реализация метода требует весьма точных вычислений. В частности, при группировке возраста в 2,3,4,5,6,7 интервалов в задаче с дихотомическими переменными – индикаторами жизненных ценностей “будущее детей”, “семья” и “материальное благосостояние” после проведения 10000 экспериментов были получены следующие значения aвыб: 5,03*10-13; 4,45*10-20; 2,62*10-14; 1,26*10-12; 2,27*10-10; 3,07*10-10. Оптимальным оказалось группирование в 3 интервала – до 28 лет, от 29 до 53 лет и старше 53 лет. Интервалы отражают, по-видимому, жизненные этапы, отражающиеся на жизненных ценностях.

2.2.1. Шкала значимости

Переход к aвыб означает введение новой сопоставимой шкалы для значений критерия Q. С использованием функции распределения aвыб вычисляется по формуле: aвыб=1-FQ(R,Y)(Qвыб(R,Y)). Если вместо Qвыб(R,Y) здесь подставить случайную величину Q(R,Y)), мы получим (в условиях независимости X и Y) равномерно распределенную случайную величину a=1-FQ(R,Y)(Q(R,Y)).

Пусть R получается в результате разбиения группы объектов по значениям переменной Xk, тогда будем называть величину ak, полученную по приведенной выше формуле, шкалой значимости Xk.

2.3. Значимость разбиения класса

Пусть для каждой группы (класса) разбиения RiÎR определена оптимальная переменная X(Ri)ÎX, по которой следует разбивать этот класс. Означает ли это, что для следующего разбиения необходимо выбрать группу Ri, для которой наблюдаемая значимость X(Ri) aвыб минимальна? Здесь многое определяет взаимосвязь переменных. Если переменные X дублируют друг друга, вероятность случайно получить лучший результат будет совпадать с этой наблюдаемой значимостью aвыб.,i=aвыб. Если переменные X независимы, целесообразно воспользоваться схемой Бонферрони и наблюдаемой значимостью считать aвыб.,i=1-(1-aвыб)m.

Если смотреть шире, критерием для выбора группы стал минимум наблюдаемой значимости по переменным Xk: amin=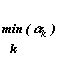, где ak – шкалы значимости Xk. Как было отмечено, для разных групп amin несравнимы из-за взаимосвязи переменных, и мы опять должны перейти к критерию значимости - вероятности случайно получить лучший результат, равной P{amin,выб>amin}. Вопрос состоит только в выяснении распределения случайной величины amin.

2.3.1. Вычисление наблюдаемой значимости группы P{amin,выб>amin}.

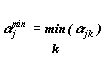Представим результаты экспериментов с генерированием Y матрицей , где Qjk – величина Q(R,Y)), полученная при агрегировании переменной Xk в j-м эксперименте. Этой матрице соответствует матрица шкал значимости . Величины представляют выборку, по которой может быть оценено распределение amin и значимость выборочного значений этой величины.

Такую оценку мы также делаем исходя из предположения бета распределения величины amin. Значения ajk могут быть вычислены по оцененному бета распределению Q(R,Y) (см. п.2.2), но проще непосредственно использовать значения . Для этого достаточно определить ранги Qjk по столбцам, тогда оценки вычисляются по следующей формуле ajk=(nexp-rjk)/nexp, где rjk – ранг Qjk.

На реальных данных, при исследовании связи жизненных ценностей с социально-демографическими характеристиками, сотня статистических экспериментов показала незначимость различия бета распределения и распределения amin (наблюдаемый уровень значимости критерия Колмогорова-Смирнова равен 0.711).

Заключение

В данной работе представлены экспериментальные результаты разработки методов, использующих множественные сравнения. Предложенные методы позволяют проводить автоматический поиск значимых связей и получать «естественную» группировку объектов, а также более точно оценивать риск ошибки в обнаружении закономерностей. В дальнейшем предполагается расширить круг закономерностей, обнаруживаемых данными методами, а также сделать программное обеспечение доступным широкому кругу исследователей.

В работе недостаточно представлены практические примеры и методика анализа данных. Мы надеемся восполнить этот пробел в будущем.

Литература

1. Аренс Х., Лейтер Ю. Многомерный дисперсионный анализ. - М.: Финансы и статистика, 1985.

2. Афифи А., Эйзен С. Статистический анализ. Подход с использованием ЭВМ.- М.:, Мир, 1982.

3. Ермаков С.М., Михайлов Г.А. Статистическое моделирование. М., Наука, 1982.

4. Лбов Г.С. Методы обработки разнотипных экспериментальных данных/ Новосибирск: Наука, 1981. 1983.

5. Петрович М.Л., Давидович М.И. Статистическое оценивание и проверка гипотез на ЭВМ.- М.: Финансы и статистика, 1989.

6. Ростовцев П.С., Костин В.С. Автоматизация типологического группирования // Препринт 137, ИЭиОПП СО РАН, Новосибирск, 1995.

7. Ростовцев П.С. Значимость и устойчивость автоматической классификации – возможность исследования при анализе археологических данных/ Методы естественных наук в археологических реконструкциях. Часть 1. - Новосибирск: Институт археологии и этнографии СО РАН, 1995.- с.59-68.

8. Ростовцев П.С. Статистические характеристики детерминации/ Статистическое моделирование экономических процессов. - Новосибирск: Наука, 1991.

9. Хастингс Н., Пикок Дж. Справочник по статистическим распределениям – М.: Статистика, 1980.

10. Чесноков С.В. Детерминационный анализ социально-экономических данных. – М.: Наука, 1988.

11. Шеффе Г. Дисперсионный анализ. – М.: Наука, 1980.

12. Tabachnick B.G., Fidell L.S. Using Multivariate Statistics. - Carolina State University, Harper Collins College Publishers, 1996. -

13. Efron B. Better bootstrap confidence intervals.//J. Amer. Statist. Ass., 81, 1986.

14. SPSS Base 7.5 for Windows.Users Guide. Chicago, 1996.

15. SPSS for Windows. Chaid. Chicago, 1996.