Жданов А.С., Костин В.С.

Значимость и устойчивость автоматической классификации в задаче поиска оптимального разбиения.

Введение

Задача проведения оптимальной (по количеству классов) автоматической классификации поставлена достаточно давно, но предложенные решения носят скорее эвристический, чем статистический характер, что оставляет вопрос об оптимальной классификации открытым [см.1,с.159-166].

Автоматическая классификация, синонимами которой можно считать термины “разбиение”, “таксономия”, “кластерный анализ”, применяется в целях получения гипотез о логической структуре изучаемой статистической совокупности объектов. Слово автоматическая подчеркивает тот факт, что разделение проводится без предварительного обучения с помощью учителя или обучающей выборки, на которой все объекты разнесены по классам. Результатом классификации является разбиение исходной совокупности объектов на некоторое число классов (таксонов, кластеров). Содержательный смысл деления на классы состоит в выделении качественно различных состояний объектов, характеризуемых своими особенными закономерностями. Дальнейшее исследование может как подтвердить, так и опровергнуть гипотезу о существовании обнаруженной кластерной структуры. Подтверждением правильности классификации является ее объяснительная и предсказательная сила при выходе за пределы исходной выборки как по признакам, так и по объектам.

Классификация применяется на предварительном этапе исследования, когда до проведения основной статистической обработки (построения регрессионных моделей, оценки параметров генеральной совокупности и т.д.) добиваются расслоения этого множества на однородные (в смысле проводимого затем статистического анализа) порции данных [см.1,с.27].

Современное состояние развития методов автоматической классификации таково, что позволяет утверждать, что она “является не столько обычным статистическим методом, сколько набором различных алгоритмов распределения объектов по кластерам. … Поэтому проверка статистической значимости в действительности здесь неприменима”[2].

В данной работе описаны несколько первых шагов на пути превращения автоматической классификации из набора алгоритмов в статистический метод, который позволит не только получать практически полезный результат, но и оценивать статистическую значимость нулевой гипотезы (об отсутствии кластерной структуры, или, что эквивалентно, - об однокластерности статистической совокупности объектов).

Следует отметить, что описываемый здесь подход является развитием идей, изложенных в публикациях [3,4]. В работе [3] описана общая постановка задачи автоматического определения оптимальной сложности разбиения для самых разных методов. В случае кластерного анализа сложность разбиения интерпретируется как количество кластеров. В монографии [4] в качестве критерия оптимальности предлагалось использовать такие показатели качества разбиения, как значимость гипотезы однокластерности и устойчивость полученной кластерной структуры, измеряемая процентом оставшихся в своих кластерах объектов при генерации повторных выборок методом Boot-Strap.

В целом продолжая предложенные подходы, мы все же несколько сместили акценты. Если результаты, полученные в монографии, можно использовать для создания статистических таблиц значимости при кластеризации по стандартизованным данным, то здесь мы напрямую (в статистических экспериментах) измеряем значимость разбиений для определения оптимального количества кластеров. Такое смещение акцента связано с существенным ростом за последние 5 лет доступных рядовому пользователю вычислительных мощностей персональных компьютеров, что делает возможным проведение полномасштабных вычислительных экспериментов в реальном времени.

Освободив показатель устойчивости классификации от его основных обязанностей – служить критерием оптимальности разбиения, авторы нашли для него новое применение - составление "структурного портрета" полученного разбиения, который выявляет взаимопереходы кластеров, их взаимодействия через обмен объектами в эспериментах с имитацией повторного сбора данных. Такие "структурные портреты" дают дополнительную информацию о кластерах, позволяя преодолеть недостатки выбранного метода кластеризации (k-средних), который является оптимальным по скорости, но накладывает существенные ограничения на форму выделяемых кластеров в виде сферических сгущений точек (объектов). Большая частота перетекания объектов между двумя соседними кластерами (межкластерная неустойчивость) дает основания выдвинуть гипотезу о единстве этих кластеров и в дальнейшем интерпретировать их как один кластер несферической формы.

Перед тем, как приступить к описанию способов определения значимости, рассмотрим кратко, что представляет из себя критерий качества разбиения и из каких шагов складывается алгоритм кластеризации. Из соображений простоты реализации и скорости выполнения нами были выбраны Евклидова метрика пространства признаков и простейший алгоритм кластеризации (k-средних), хотя способ измерения значимости не накладывает особых ограничений ни на метрику, ни на сам алгоритм. Но все же необходимо отметить, что к поведению алгоритма предъявляются повышенные требования, поэтому мы были вынуждены внести в него некоторые изменения, которые позволили улучшить качество разбиения и, как побочный эффект, сократить время вычислений (за счет уменьшения количества итераций).

Критерий качества разбиения

Результатом кластерного анализа является разбиение имеющихся в исходной выборке объектов на некоторое количество кластеров. При этом каждый кластер включает в свой состав один или более объектов. Мы будем описывать кластер не просто как множество объектов, а как некий идеальный объект, имеющий свои координаты в пространстве признаков. Принимаем, далее, что эти координаты являются арифметическим средним координат реальных объектов, входящих в состав кластера, то есть координаты кластера совпадают с координатами его центра.

Теперь зададимся вопросом, что будет, если мы, вместо реальных координат объекта, будем использовать координаты кластера, к которому он отнесен? Очевидно, при этом мы теряем часть информации об объекте, поскольку внутри кластеров объекты не идентичны. Но, чем лучше кластерная структура описывает реальные скопления объектов в признаковом пространстве, тем меньшая часть информации будет потеряна и тем большую ее часть будет нести в себе кластер, как представитель всех принадлежащих ему объектов.

Исходя из этих соображений, логично выбрать критерием качества кластеризации какую-либо характеристику потерь информации при описании объектов кластерами. Наиболее простой оценкой таких потерь является остаточная дисперсия, представляющая собой сумму квадратов отклонений объектов от центров их кластеров. Если же мы хотим иметь дело с безразмерной величиной, то наиболее удобным будет нормировать эту величину на остаточную дисперсию однокластерной структуры. Полученная таким образом доля остаточной дисперсии принимает значения в диапазоне от нуля до единицы. Чем лучше качество разбиения, тем ближе она к нулю, и наилучшему разбиению на кластеры будет соответствовать минимум доли остаточной дисперсии. А сама эта величина напрямую показывает, какую часть информации мы потеряем при замене объектов на кластеры.

Алгоритм кластеризации

Поскольку способ измерения значимости гипотезы отсутствия кластерной структуры требует проведения кластеризации не только на исходных данных, но и на десятках, сотнях случайно сгенерированных выборок, требования к скорости алгоритма по сравнению с традиционным кластерным анализом существенно ужесточаются. С учетом этого обстоятельства выбор метода k-средних становится почти вынужденным.

Но измерение значимости требует от алгоритма не только скорости, но и "хорошего поведения", поскольку значимость определяется при сравнении остаточной дисперсии на исходных данных с усредненной остаточной дисперсией в статистических экспериментах (малая разность двух больших величин намного более чувствительна к ошибкам, чем сами эти величины). Мало того, нас интересует не просто значимость сама по себе, а минимум значимости при изменении количества кластеров от двух до некоторого предельного значения. Мы можем позволить себе ошибиться в величине значимости при некотором k, но не должны допускать ошибки при сравнении значимостей на разных количествах кластеров. Таким образом, от алгоритма требуется по меньшей мере монотонность критерия при увеличении количества кластеров, а также как можно меньший дефект алгоритма (в данном случае - это "недожатая", по сравнению с глобальным минимумом, доля остаточной дисперсии, которая вносит дополнительный шум в оценку значимости).

Исходный метод k-средних можно разложить на следующие 4 шага:

1) случайно выбираются k объектов - центров кластеров;

2) каждый объект относится к ближайшему кластеру (по расстоянию до центра);

3) вычисляются новые центры кластеров - средние арифметические по объектам;

4) если произошло уменьшение критерия качества кластеризации - осуществляется переход к п.2).

Самый слабый пункт в этом алгоритме (и единственный, подлежащий модификации без качественного изменения идеи алгоритма) - это первый шаг. Поскольку метод дает не глобальный, а локально-оптимальный результат, то и качество разбиения, и скорость зависят в решающей степени от удачного начального разбиения.

В описанный алгоритм было внесено 2 изменения, хотя резервы улучшения этим далеко не исчерпаны. Во-первых, учитывая то, что поиск оптимального количества кластеров требует последовательного проведения кластеризации для диапазона значений k>1, мы решили не отбрасывать результат предыдущего разбиения на k кластеров, а использовать полученные центры в качестве начального приближения на k+1 шаге. Эта модификация позволила исключить случаи немонотонного уменьшения остаточной дисперсии с ростом количества кластеров. Во-вторых, для определения k+1 кластера мы берем не пустое множество, как предлагалось в [4], а поступаем следующим образом. Среди k кластеров находим такой, который при разбиении на два дает наибольший эффект уменьшения критерия. Эти две части кластера и дают координаты k-го и k+1-го кластеров.

Оценка значимости

Критерий качества разбиения, описанный выше, позволяет определить оптимальное разбиение при заданном количестве кластеров, но не может служить основанием для сравнения внутри ряда оптимальных разбиений. Это связано с тем, что значение этого критерия при возрастании количества кластеров ведет себя как монотонно убывающая функция (пока не достигнет нуля), но мы не располагаем информацией, насколько быстро она должна убывать. Для получения такой информации мы ввели в качестве эталона для сравнения случайно сгенерированную, в соответствии с нулевой гипотезой, выборку данных того же объема, что и исходная. Нулевая гипотеза заключается в том, что распределение объектов в пространстве признаков соответствует многомерной нормальности. При этом длины осей эллипсоида рассеяния для случайной выборки совпадают с таковыми в исходной. В дальнейшем тексте нулевую гипотезу будем называть гипотезой однокластерной структуры или гипотезой отсутствия кластерной структуры.

Для определения оптимального количества кластеров мы использовали оценку значимости гипотезы однокластерной структуры. Минимум значимости достигается на числе кластеров, которое дает наиболее отклоняющуюся (в сторону меньших значений) долю остаточной дисперсии на исходных данных по сравнению со средним значением доли остаточной дисперсии в статистических экспериментах.

При разработке алгоритма оценки значимости необходимо принять два решения:

· Как генерировать случайную выборку с однокластерной структурой (по построению), которая была бы по остальным параметрам сравнима с исходной выборкой;

· Как измерять значимость гипотезы однокластерности, располагая значениями критерия качества разделения (при k кластерах) на исходных данных и для всего множества случайных выборок.

Рассмотрим эти проблемы по порядку.

В монографии предлагалось имитировать однокластерную структуру выборкой, нормально распределенной в сферически симметричной области, а сами исходные данные преобразовывать к такому виду с помощью ориентации в многомерном пространстве вдоль главных компонентов (найденных факторным анализом). Поскольку при этом мы получаем облако рассеяния в виде многомерного эллипсоида, то следующим шагом растягиваем его оси так, чтобы их длина стала одинаковой, то есть превращаем эллипсоид в сферу. Такой подход страдает несколькими недостатками. Во-первых, при переходе к главным компонентам размерность пространства может уменьшиться за счет линейной зависимости выбранных переменных, а во-вторых, после растягивания осей мы меняем метрику пространства и в результате ищем уже совсем не ту кластерную структуру, которую обнаружили бы в исходном пространстве. Таким образом, решая задачу оценки значимости отсутствия кластерной структуры, нам пришлось бы накладывать слишком жесткие ограничения на саму процедуру кластеризации.

Учитывая указанные недостатки, мы пришли к альтернативному решению - преобразовывать не исходные данные к сферическому распределению, а генерировать случайные выборки в эллипсоиде, длины осей которого совпадают с главными компонентами. При этом оси нулевой длины не приносят неприятностей (умножать на ноль всегда проще, чем делить), а на процедуру кластеризации не накладывается дополнительных ограничений.

Теперь перейдем к вопросу измерения значимости гипотезы однокластерности. Поскольку критерием качества кластеризации была выбрана доля остаточной дисперсии, которая принимает значения от нуля до единицы, то естественно будет аппроксимировать распределение значений этого критерия в серии случайных экспериментов Бэта-распределением, которое работает для случайных величин, имеющих ограниченную с обоих сторон область допустимых значений:

(1)

Параметры a и b Бэта-распределения легко определить по выборочному среднему M и дисперсии D:

	(2)
	(3)

Получив оценки параметров Бэта-распределения, мы можем вычислить значимость гипотезы однокластерности при любом значении x(k) - доли остаточной диперсии на k кластерах. Значимость вычисляется как интеграл Бэта-распределения в пределах от нуля до остаточной дисперсии d(k):

(4)

Учет микро-кластеров

Итак, мы имеем способ генерации случайной выборки и способ измерения значимости гипотезы однокластерности. Казалось бы, этого достаточно, чтобы считать метод определения оптимального количества кластеров готовым к применению. Однако пробные расчеты на реальных данных показали, что это далеко не так. Оказалось, что не существует данных, на которых этот метод в чистом виде дал бы ожидаемый результат - оптимальное количество кластеров. Авторы столкнулись с эффектом систематического уменьшения значимости при увеличении количества кластеров вплоть до n-1 (n - количество объектов в выборке). Получалось, что в области практически интересного количества кластеров минимум значимости не локализуется.

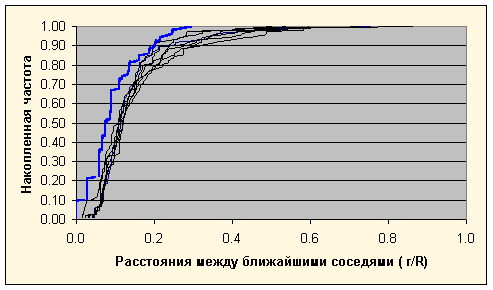
Поиск причины появления "хвоста значимости" немедленно привел к исследованию распределения межобъектных расстояний. Построение графика распределения расстояний между ближайшими соседями выявило резкое отличие этого распределения на реальных данных от аналогичного распределения на случайных. А именно - в реальных выборках распределение систематически смещено в область нулевых расстояний, то есть наблюдается повышенное содержание "слипшихся точек", которые образуют множество "микро-кластеров", состоящих из 2-3 объектов.

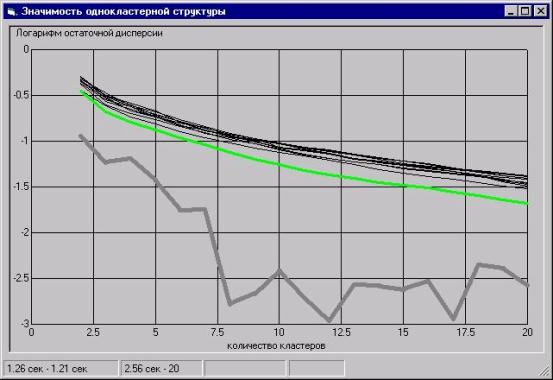
Что является причиной повышенной концентрации "слипшихся точек" в реальных данных, остается открытым вопросом, однако одна гипотеза все же есть. Согласно этой гипотезе, причина кроется в ограниченной точности измерения данных (в отличие от практически неограниченной точности представления случайных данных), которая наблюдается в одномерных распределениях значений в виде многократно повторяющихся значений (дублей). Таким образом, здесь мы, возможно, сталкиваемся со статистическим "квантовым порогом", за пределами которого предположения о непрерывности распределения становятся неприменимыми, что и приводит к катастрофе классического подхода.

Какие способы выхода из этой ситуации можно предложить? Их по крайней мере три:

1. Скорректировать случайные данные так, чтобы на них распределение расстояний между ближайшими соседями не отличалось от того же распределения на исходных данных;

2. Скорректировать исходные данные так, чтобы на них распределение расстояний между ближайшими соседями не отличалось от того же распределения на случайных данных, то есть искусственно рандомизировать исходные данные, разрушив микро-кластеры;

3. И последнее - генерировать случайные данные с учетом реальных одномерных распределений и ковариационной матрицы. При этом все "квантовые эффекты" будут гарантированно скопированы с исходных данных.

Каждый из этих способов обладает своими достоинствами и недостатками, в частности, третий способ требует дополнительной проработки и пока остается непроверенным.

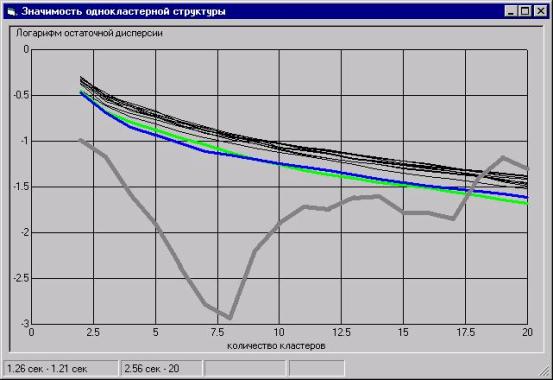
В качестве рабочего варианта мы выбрали второй способ, то есть корректировку исходных данных (только для оценки значимости, но не для получения кластерной структуры), которая эффективно отбрасывает хвост значимости наверх и дает возможность проявиться минимуму значимости при разумных k.

Дефекты алгоритма

Алгоритм определения значимости нулевой гипотезы (отсутствия кластерной структуры) в том виде, как он здесь описан, обладает существенным недостатком: он вносит большой шум в измеряемую им значимость, и величина этого шума уменьшается только с ростом числа статистических экспериментов. В то же время, из-за высокой вычислительной сложности проводимых экспериментов, мы не можем себе позволить добиться приемлемой точности измерения методом грубой силы.

Рассмотрим несколько подробнее основные источники шума. Для этого необходимо проанализировать способ измерения значимости. Из уравнения 4 видно, что значимость нулевой гипотезы является преобразованным значением остаточной дисперсии, и определяющую роль в этом преобразовании играют параметры a(k) и b(k), которые, в свою очередь (уравнения 2,3), полностью определяются статистическими параметрами распределения M(k) и D(k) значений остаточной дисперсии по всем проведенным экспериментам. Итак, мы пришли к пониманию того, что шум измерения имеет своим источником статистический разброс параметров M(k) и D(k).

Теперь, зная источник шума, попробуем наметить (на будущее) подходы к его уменьшению:

1. Увеличение количества проводимых экспериментов (метод грубой силы):

2. Сглаживание рядов M(k) и D(k) при помощи цифровых фильтров:

3. Экспериментальное исследование зависимостей M и D от k с определением класса функций для их аппроксимации и аппроксимация рядов этими функциями путем подбора параметров.

Самым перспективным нам представляется последний подход, который, однако, требует дополнительного времени на исследование.

Следует отметить, что и само значение остаточной дисперсии, как предел интегрирования в уравнении 4, также является источником шума, причина которого кроется в дефекте алгоритма кластеризации, направленного на поиск локального, а не глобального минимума остаточной дисперсии, за счет чего остаточная дисперсия "не выжимается на все 100%", и эта "недожатая" дисперсия порождает дополнительный разброс величины критерия как в исходных данных, так и в статистических экспериментах.

Неустойчивость классификации как проявление межкластерных связей

Если в монографии [4] интегральный показатель устойчивости классификации предлагалось использовать как критерий выбора оптимального количества кластеров, то в настоящей работе эта ниша занята показателем значимости гипотезы однокластерности. Но это не означает, что исследование устойчивости утратило необходимость. Напротив, определилась задача, в решении которой результаты измерений устойчивости (а правильнее было бы сказать - неустойчивости) оказываются применимы напрямую.

Эта задача связана с преодолением недостатка выбранного в данной работе метода кластеризации (k-средних). Дело в том, что метод k-средних накладывает определенные ограничения на форму выделяемых кластеров, источником которых (ограничений) является критерий оптимальности искомой структуры в виде минимума внутрикластерного разброса. Поскольку этот разброс вычисляется по расстояниям от центра кластера, до всех объектов, входящих в этот кластер, то в результате форма выделяемых кластеров получается близкой к сферической. Но в тех случаях, когда прообразы кластеров в признаковом пространстве оказываются вытянутыми или тороидальными (для циклически протекающих процессов), метод k-средних, в лучшем случае, выдаст цепочку следующих друг за другом шарообразных кластеров.

Восстановление исходной формы (и количества) кластеров, искаженных описанным недостатком алгоритма, и является той задачей, которая в данной работе возложена на описательную статистику неустойчивости кластерной структуры. Показатель неустойчивости определяется как доля объектов, перебегающих (в среднем) между каждой парой кластеров, и представляется графически в виде отрезка, соединяющего центры кластеров. Ширина отрезка пропорциональна показателю неустойчивости. Кластеры, соединенные самыми широкими полосами неустойчивости, являются первыми кандидатами на объединение в один класс. Правомерность такого объединения требует подтверждения независимыми методами, а потому является только гипотетическим.

В заключение авторы выражают благодарность П.С.Ростовцеву за многочисленные полезные обсуждения и выдвинутую им гипотезу о квантованном характере реальных измерений как причине появления "слипшихся точек".

Литература

1. Прикладная статистика: Классификация и снижение размерности: Справочное издание. / С.А.Айвазян, В.М.Бухштабер, И.С.Енюков, Л.Д.Мешалкин; Под рад. С.А.Айвазяна. – М.: Финансы и статистика, 1989. – 607с.: ил.

2. Электронный учебник StatSoft. Кластерный анализ. http:/ns.dsmu.donetsk.ua/~statbook/modules/stcluan.html

3. П.С.Ростовцев Определение сложности структуры агрегирования данных на основе статистических критериев. В сб. Алгоритмы анализа данных социально-экономических исследований. Под ред. Б.Г.Миркина. Новосибирск, 1982

4. П.С.Ростовцев 7.2.Методы автоматизации типологического анализа археологических данных. В монографии: Математические методы в археологических реконструкциях. Методология и методика археологических реконструкций. Отв. ред. А.П.Деревянко, Ю.П.Холюшкин. Новосибирск, 1995